题目内容
9.半径为r带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图1所示.有一变化的磁场垂直于纸面,规定向内为正,变化规律如图2所示.在t=0时刻平板之间中心有一重力不计,质量为m,电荷量为+q的静止微粒,微粒在运动过程中不会与AB板发生碰撞,则:
(1)t1=0.5s时两板电势差UAB
(2)第一秒末微粒的速度
(3)0到3.5s微粒的位移大小.
分析 (1)由法拉第电磁定律求解两板电势差UAB.
(2)由楞次定律可以判断出两极板哪个是正极,哪个是负极;由匀强电场场强与电势差的关系U=Ed可以求出两极板间的场强大小,由牛顿第二定律求出微粒的加速度,由速度公式求解即可.
(3)分析微粒的运动情况,由牛顿第二定律和运动学公式结合解答.
解答 解:(1)两板电势差等于圆环产生的感应电动势.根据法拉第电磁感应定律可得两极板间的电势差为:
UAB=$\frac{△B}{△t}$πr2=1×π×r2=πr2
(2)第1s内,磁感应强度均匀增大,根据楞次定律知,上极板带负电,下极板带正电,微粒向上做匀加速运动,则加速度为:
a=$\frac{q{U}_{AB}}{md}$=$\frac{qπ{r}^{2}}{md}$
第一秒末微粒的速度为:
v=at=$\frac{qπ{r}^{2}}{md}$
(3)第1s内下极板为正极,微粒向上做匀加速直线运动,第2s内,上极板为正极,微粒做匀减速直线运动到零,第3s回微粒向下做匀加速直线运动,第4s内,微粒向下做匀减速直线运动到零,根据运动过程的对称性,可知第4s末回到原位置.0到3.5s微粒的位移等于3.5s到4s内的位移大小,运用逆向思维可得0到3.5s微粒的位移为:
x=$\frac{1}{2}a(0.5)^{2}$=$\frac{qπ{r}^{2}}{8md}$
答:(1)t1=0.5s时两板电势差UAB为πr2.
(2)第一秒末微粒的速度为$\frac{qπ{r}^{2}}{md}$.
(3)0到3.5s微粒的位移大小为$\frac{qπ{r}^{2}}{8md}$.
点评 本题是一道综合题,关键要掌握楞次定律、法拉第电磁感应定律、匀强磁场场强与电势差的关系式U=Ed,可作出v-t图象分析微粒的运动情况,由力学规律求解速度和位移.

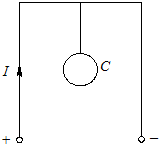 如图所示,一根长导线弯曲成“п”,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
如图所示,一根长导线弯曲成“п”,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )| A. | 金属环中无感应电流产生 | B. | 金属环中有顺时针方向的感应电流 | ||
| C. | 悬挂金属环C的竖直线中拉力变大 | D. | 金属环C仍能保持静止状态 |
| A. | 若分子间的距离增大,则分子间的引力增大,斥力减小 | |
| B. | 若分子间的距离减小,则分子间的引力和斥力均增大 | |
| C. | 若分子间的距离减小,则分子间引力和斥力的合力将增大 | |
| D. | 若分子间的距离增大,则分子间引力和斥力的合力将减小 |
 法拉第发明了世界上第一台发电机法拉第圆盘发电机.如图所示,紫铜做的圆盘水平放置在竖直向下的匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各与一个黄铜电刷紧贴,用导线将电刷与电流表连接起来形成回路.转动摇柄,使圆盘逆时针匀速转动,电流表的指针发生偏转.下列说法正确的是( )
法拉第发明了世界上第一台发电机法拉第圆盘发电机.如图所示,紫铜做的圆盘水平放置在竖直向下的匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各与一个黄铜电刷紧贴,用导线将电刷与电流表连接起来形成回路.转动摇柄,使圆盘逆时针匀速转动,电流表的指针发生偏转.下列说法正确的是( )| A. | 回路中电流大小变化,方向不变 | |
| B. | 回路中电流大小不变,方向变化 | |
| C. | 回路中电流的大小和方向都周期性变化 | |
| D. | 回路中电流方向不变,从b导线流进电流表 |

| A. | 甲在往负方向运动 | B. | 甲、乙两物体相向运动 | ||
| C. | 甲做匀加速运动,乙做匀减速运动 | D. | 5s末两物体速度相同 |
 质谱仪是测带电粒子质量和分析同位素的一种仪器,如图所示.它的工作原理是带电粒子(不计重力)经同一电场加速后,垂直进入同一匀强磁场做圆周运动,然后利用相关规律计算出带电粒子质量.图中虚线为某粒子运动轨迹,由图可知( )
质谱仪是测带电粒子质量和分析同位素的一种仪器,如图所示.它的工作原理是带电粒子(不计重力)经同一电场加速后,垂直进入同一匀强磁场做圆周运动,然后利用相关规律计算出带电粒子质量.图中虚线为某粒子运动轨迹,由图可知( )| A. | 此粒子带负电 | |
| B. | 下极板S2比上极板S1电势高 | |
| C. | 若只增大加速电压U,则半径r变大 | |
| D. | 若只增大入射粒子的质量,则半径r变小 |
 如图所示,有人用一簇气球通过绳使一座小屋成功升空.成为“会飞的小屋”.下列说法正确的是( )
如图所示,有人用一簇气球通过绳使一座小屋成功升空.成为“会飞的小屋”.下列说法正确的是( )| A. | 小屋受到绳的拉力和小屋对绳的拉力是一对作用力和反作用力 | |
| B. | 小屋受到绳的拉力和小屋所受重力是一对作用力和反作用力 | |
| C. | 小屋对绳的拉力和小屋所受重力是一对作用力和反作用力 | |
| D. | 小屋对绳的拉力和小屋所受重力是一对平衡力 |
 油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.6mL.用滴管向量筒内滴50滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成单分子油膜的形状如图所示.
油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.6mL.用滴管向量筒内滴50滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成单分子油膜的形状如图所示. AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求: