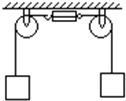
题目内容
 如图所示,一条轻绳两端各系着质量为m1=4kg和m2=1kg的两个小物体,通过定滑轮悬挂在车厢顶上,绳与滑轮的摩擦忽略不计.若车以加速度a=5m/s2向右运动,m1仍然与车厢地板相对静止,试求:
如图所示,一条轻绳两端各系着质量为m1=4kg和m2=1kg的两个小物体,通过定滑轮悬挂在车厢顶上,绳与滑轮的摩擦忽略不计.若车以加速度a=5m/s2向右运动,m1仍然与车厢地板相对静止,试求:(1)此时绳上的张力T.
(2)m1与地板之间的摩擦因数μ至少要多大?
分析:(1)当车以加速度a=5m/s2向右运动时,悬挂m2的绳子与竖直方向的夹角不变,设为θ,m1相对于车厢静止,其加速度与车厢相同.以m2为研究对象,分析受力,根据牛顿第二定律和力的合成求出绳上的张力T.
(2)再以m1为研究对象,分析受力,根据牛顿第二定律,运用正交分解法求解车厢底板对m1的支持力和静摩擦力.静摩擦力应小于等于最大静摩擦力,列式可求出μ至少多大.
(2)再以m1为研究对象,分析受力,根据牛顿第二定律,运用正交分解法求解车厢底板对m1的支持力和静摩擦力.静摩擦力应小于等于最大静摩擦力,列式可求出μ至少多大.
解答: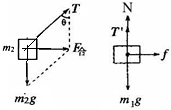 解:(1)以m2为研究对象,分析受力,如图所示,根据牛顿第二定律和力的合成得
解:(1)以m2为研究对象,分析受力,如图所示,根据牛顿第二定律和力的合成得
T=
=
=1×
N=5
N.
(2)再以m1为研究对象,分析受力,根据牛顿第二定律,得
f=m1a
N+T′=m1g
又T′=T
解得,f=20N,N=(40-5
)N
要使m1与地板保持相对静止,则必须有 f≤fm=μN
解得μ≥
答:(1)此时绳上的张力T为5
N.
(2)m1与地板之间的摩擦因数μ至少为
.
 解:(1)以m2为研究对象,分析受力,如图所示,根据牛顿第二定律和力的合成得
解:(1)以m2为研究对象,分析受力,如图所示,根据牛顿第二定律和力的合成得T=
(m2g)2+
|
| (m2g)2+(m2a)2 |
| 102+52 |
| 5 |
(2)再以m1为研究对象,分析受力,根据牛顿第二定律,得
f=m1a
N+T′=m1g
又T′=T
解得,f=20N,N=(40-5
| 5 |
要使m1与地板保持相对静止,则必须有 f≤fm=μN
解得μ≥
32+4
| ||
| 59 |
答:(1)此时绳上的张力T为5
| 5 |
(2)m1与地板之间的摩擦因数μ至少为
32+4
| ||
| 59 |
点评:本题属于知道受力情况求解运动情况的类型,关键是分析受力情况,运用牛顿第二定律求解即可.

练习册系列答案
相关题目
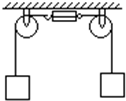 如图所示,一条轻绳跨过两个光滑定滑轮,绳的两端挂着砝码,每个砝码的重力均为50N,把滑轮间的绳剪断后接入一个弹簧秤.(弹簧秤的重力忽略不计)试求:
如图所示,一条轻绳跨过两个光滑定滑轮,绳的两端挂着砝码,每个砝码的重力均为50N,把滑轮间的绳剪断后接入一个弹簧秤.(弹簧秤的重力忽略不计)试求: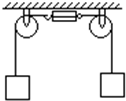 如图所示,一条轻绳跨过两个光滑定滑轮,绳的两端挂着砝码,每个砝码的重力均为50N,把滑轮间的绳剪断后接入一个弹簧秤.(弹簧秤的重力忽略不计)试求:
如图所示,一条轻绳跨过两个光滑定滑轮,绳的两端挂着砝码,每个砝码的重力均为50N,把滑轮间的绳剪断后接入一个弹簧秤.(弹簧秤的重力忽略不计)试求: