Question

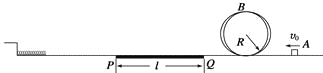
【题目】如图，在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道，水平轨道的PQ段铺设特殊材料，调节其初始长度为l，水平轨道左侧有一轻质弹簧左端固定，弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道，通过圆形轨道、水平轨道后压缩弹簧，并被弹簧以原速率弹回。已知R＝0．4 m，v0＝6 m/s，物块质量m＝1 kg，与PQ段间的动摩擦因数μ＝0．4，轨道其它部分摩擦不计。取g＝10 m/s2。求：

（1）物块第一次经过圆轨道最高点B时对轨道的压力；

（2）物块仍以v0从右侧冲上轨道，调节PQ段的长度l，当l长度是多少时，物块恰能不脱离轨道返回A点继续向右运动。

Answer 1

【答案】（1）40N，方向竖直向上（2）L=1m

【解析】试题分析：（1）物块冲上圆形轨道最高点B时速度为v，由机械能守恒得： mv02＝mv2+2mgR

物块到B点，由牛顿运动定律得：N+mg＝m

联立①②式并代入数据解得N=40N

由牛顿第三定律，物块对轨道压力大小为40N，方向为竖直向上

（2）物块以v0冲上轨道直到回到PQ段右侧Q点时速度为v2，有2μmgl＝mv22mv02

要使物块恰能不脱离轨道返回A点，则物块能沿轨道上滑至最高点且在最高点的速度大小为v3，则满足mv22＝2mgR+mv32

且mg＝m

联立各式代入数据解得：L="1" m