题目内容
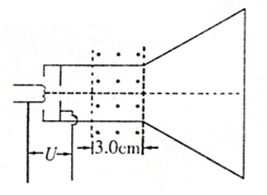 在电脑显示器的真空示波管内,控制电子束扫描的偏转场是匀强磁场,磁场区域是宽度为3.0cm的矩形,右边界距荧光屏20.0cm,高度足够.某段时间内磁场方向垂直纸面向外,磁感应强度B=4.55×10-3T不变.电子初速度不计,经U=4550V电压加速后沿中心线射入磁场,偏转后打在屏上产生亮点(若无磁场,亮点在屏中心),已知电子的质量m=0.91×10-30kg,电荷量e=1.6×10-19C.
在电脑显示器的真空示波管内,控制电子束扫描的偏转场是匀强磁场,磁场区域是宽度为3.0cm的矩形,右边界距荧光屏20.0cm,高度足够.某段时间内磁场方向垂直纸面向外,磁感应强度B=4.55×10-3T不变.电子初速度不计,经U=4550V电压加速后沿中心线射入磁场,偏转后打在屏上产生亮点(若无磁场,亮点在屏中心),已知电子的质量m=0.91×10-30kg,电荷量e=1.6×10-19C.(1)在图中大致图出电子运动的径迹;
(2)求亮点偏离荧光屏中心的距离.
分析:(1)电子在电场中做直线运动,在磁场中由左手定则判断洛伦兹力方向向上,则电子向上偏转;
(2)先由动能定理求出粒子离开电场时获得的速度,然后由牛顿第二定律求出粒子在磁场 中圆周运动的半径,亮点偏离荧光屏中心的距离为磁场中竖直方向偏离的距离与做匀速直线运动过程竖直方向的位移之和.
(2)先由动能定理求出粒子离开电场时获得的速度,然后由牛顿第二定律求出粒子在磁场 中圆周运动的半径,亮点偏离荧光屏中心的距离为磁场中竖直方向偏离的距离与做匀速直线运动过程竖直方向的位移之和.
解答:解:(1)电子运动的径迹如图所示:
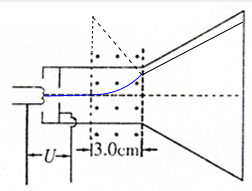
(2)电子经U加速得到速度v0
由eU=
mv 02
得v0=
=
m/s=4×107m/s.
由evB=m
得 ①
r=
=
m=0.05m=5cm ②
sinα=
,cosα=
,tanα=
③
亮点偏离屏中心的距离:
y=(r-rcosα)+20.0tanα=5×(1-
)cm+20.0×
cm=16cm;
答:(1)在图中大致图出电子运动的径迹如图;(2)亮点偏离荧光屏中心的距离为16cm.

(2)电子经U加速得到速度v0
由eU=
| 1 |
| 2 |
得v0=
|
|
由evB=m
| v02 |
| r |
r=
| mv0 |
| Be |
| 0.91×10-30×4×107 |
| 4.55×10-3×1.6×10-19 |
sinα=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
亮点偏离屏中心的距离:
y=(r-rcosα)+20.0tanα=5×(1-
| 4 |
| 5 |
| 3 |
| 4 |
答:(1)在图中大致图出电子运动的径迹如图;(2)亮点偏离荧光屏中心的距离为16cm.
点评:该题涉及到带电粒子在电场和磁场的运动情况,对同学们的分析能力和数学功底要求较高,关键是要有耐心,正确画出轨迹后充分结合数学知识即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
