题目内容
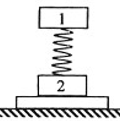
 如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则有( )
如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则有( )分析:木板抽出前,木块1和木块2都受力平衡,根据共点力平衡条件求出各个力;木板抽出后,木板对木块2的支持力突然减小为零,其余力均不变,根据牛顿第二定律可求出两个木块的加速度.
解答:解:在抽出木板的瞬时,弹簧对1的支持力和对2的压力并未改变.对1物体受重力和支持力,mg=F,a1=0.
对2物体受重力和弹簧的向下的压力,根据牛顿第二定律
a=
=
g
故选C.
对2物体受重力和弹簧的向下的压力,根据牛顿第二定律
a=
| F+Mg |
| M |
| M+m |
| M |
故选C.
点评:本题属于牛顿第二定律应用的瞬时加速度问题,关键是区分瞬时力与延时力;弹簧的弹力通常来不及变化,为延时力,轻绳的弹力为瞬时力,绳子断开即消失.

练习册系列答案
相关题目
 如图,轻弹簧上端与一质量为3m的木块1相连,下端与另一质量为m的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则有( )
如图,轻弹簧上端与一质量为3m的木块1相连,下端与另一质量为m的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则有( )| A、a1=g,a2=g | ||
B、a1=0,a2=
| ||
| C、a1=0,a2=4g | ||
| D、a1=g,a2=3g |
 如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则a1=
如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则a1=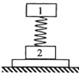 如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则有( )
如图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g.则有( ) 、
、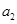 。重力加速度大小为g。则有
。重力加速度大小为g。则有 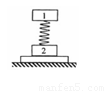
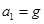 ,
,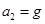 B.
B.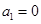 ,
,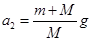 D.
D.