Question

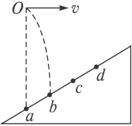
如图5-3-13所示，半径R=0.40 m的光滑半圆环轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10 kg的小球，以初速度v₀=7.0 m/s在水平地面上向左做加速度a=3.0 m/s²的匀减速直线运动，运动4.0 m后，冲上竖直半圆环，最后小球落在C点.求A、C间的距离（取重力加速度g=10 m/s²）.

图5-3-13

Answer 1

解析：匀减运动过程中，有：

v_A²-v₀²=-2as

    恰好做圆周运动时物体在最高点B满足：

mg=  v_m=2 m/s

    假设物体能到达圆环的最高点B，由机械能守恒：mv_A²=2mgR+mv_b²，可得v_B=3 m/s，因为v_B＞v_m，所以小球能通过最高点B.小球从B点做平抛运动，有2R=gt²  s_AC=v_B·t

由以上可得：s_AC=1.2 m.

答案：s_AC=1.2 m