题目内容
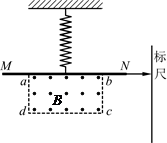
（15分）如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1 m，导轨平面与水平面成θ = 37°角，下端连接阻值为R＝2Ω的电阻。磁场方向垂直导轨平面向上，磁感应强度为0.4T。质量为0.2kg、电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为0.25。金属棒沿导轨由静止开始下滑。(g=10m/s2，sin37°＝0.6，cos37°＝0.8)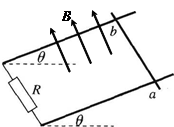 
(1)判断金属棒下滑过程中产生的感应电流方向；
(2)求金属棒下滑速度达到5m/s时的加速度大小；
(3)当金属棒下滑速度达到稳定时，求电阻R消耗的功率。
见解析
解析试题分析：(1)由右手定则判断金属棒中的感应电流方向为由a到b （2分）
(2) 金属棒下滑速度达到5 m/s时产生的
感应电动势为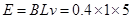
V = 2V ……（1分）
感应电流为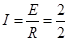 
A = 1A ……（1分）
金属棒受到的安培力为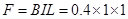
N =" 0.4" N ……（1分）
由牛顿第二定律得：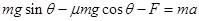
……（2分）
解得：a = 2m/s2 ……（2分）
(3)设金属棒运动达到稳定时，所受安培力为F/，棒在沿导轨方向受力平衡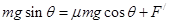
（2分）
解得：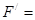
0.8 N （2分）
此时感应电流为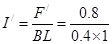
A = 2A （2分）
电路中电阻R消耗的电功率：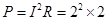
W = 8W （2分）
（另解：由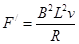
，解得稳定时速度达到最大值
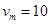m/s，本题克服安培力做功功率等于电阻R消耗的电功率，所以
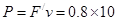W=8W）
考点：导体棒切割磁感线时的感应电动势，共点力平衡的条件及其应用，牛顿第二定律，电磁感应中的能量转化
练习册系列答案
相关题目
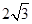kg的木块A套在水平杆上，并用轻绳将木块A与质量m＝
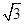kg的小球相连，今用跟水平方向成α＝30°角的力F＝
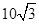N，拉着球带动木块一起向右匀速运动，运动中M、m相对位置保持不变，取g＝10m/s2，求：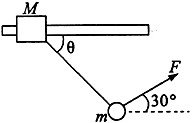
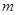，塔基宽度为d。相邻铁塔间输电线的长度为L，其单位长度的质量为
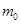，输电线顶端的切线与竖直方向成
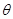角。已知冰的密度为
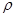，设冰层均匀包裹输电线上，且冰层的横截面为圆形，其半径为R(输电线的半径可忽略)
的光滑斜面P上有两个用轻质弹簧相连的物块A、B；C为一垂直固定在斜面上的挡板.P、C总质量为M，A、B质量均为m，弹簧的劲度系数为k，系统静止于光滑水平面.现开始用一水平力F从零开始增大作用于P. 求：
下列关于惯性的说法中，正确的是（ ）
| A．物体仅在静止和匀速运动时才具有惯性 |
| B．歼击机战斗前抛掉副油箱是为了减小惯性、提高灵活性 |
| C．物体的速度越大其惯性越大；物体的速度越小则其惯性越小 |
| D．质量相同的物体在月球上比在地球上的惯性小 |