题目内容
14.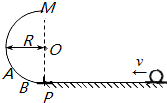 如图所示,竖直平面内有半径为R的半圆形轨道,其直径MP与水平面垂直,在P处另接一水平轨道后,放在水平桌面上,使质量为m的小球在水平轨道上以一定的速度启动.若轨道无摩擦,小球恰好能滚过M点;若轨道在B点以下是有摩擦的,那么小球只能滚到图中的A点,OA与OP夹角为60°,求在第二种情况中,小球在运动到A点的过程中,克服摩擦阻力所做的功.
如图所示,竖直平面内有半径为R的半圆形轨道,其直径MP与水平面垂直,在P处另接一水平轨道后,放在水平桌面上,使质量为m的小球在水平轨道上以一定的速度启动.若轨道无摩擦,小球恰好能滚过M点;若轨道在B点以下是有摩擦的,那么小球只能滚到图中的A点,OA与OP夹角为60°,求在第二种情况中,小球在运动到A点的过程中,克服摩擦阻力所做的功.
分析 若轨道无摩擦,小球恰好能滚过M点,根据牛顿运动定律和动能定理列方程,若轨道在B点以下是有摩擦的,那么小球只能滚到图中的A点,OA与OP夹角为60°,则末速度为零,根据动能定理列方程.
解答 解:若轨道无摩擦,小球恰好能滚过M点,则有:
mg=m$\frac{{v}_{M}^{2}}{R}$…①
-2mgR=$\frac{1}{2}m{v}_{M}^{2}$-$\frac{1}{2}m{v}_{p}^{2}$…②
若轨道在B点以下是有摩擦的,那么小球只能滚到图中的A点,OA与OP夹角为60°,
有动能定理知:Wf-mg(R-Rcos60°)=0-$\frac{1}{2}m{v}_{P}^{2}$…③
由①②③解得:Wf=-2mgR
答:小球在运动到A点的过程中,克服摩擦阻力所做的功为2mgR.
点评 本题是向心力知识和动能定理的综合应用,对于向心力,关键通过分析受力,确定向心力的来源,并能把握最高点的临界条件.

练习册系列答案
相关题目
4.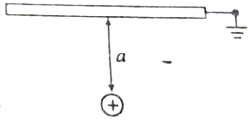 如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )
如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )
 如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )
如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )| A. | 2a$\sqrt{\frac{mg}{k}}$ | B. | a$\sqrt{\frac{mg}{k}}$ | C. | 无穷大 | D. | 0 |
5.卢瑟福在研究α粒子轰击金箔的实验中,根据实验现象提出原子的核式结构.以下说法正确的( )
| A. | 按照汤姆孙模型,α粒子轰击金箔时不可能发生大角度的偏转,因而卢瑟福否定了汤姆孙的“枣糕模型”,提出新的原子结构模型 | |
| B. | 绝大多数α粒子穿过金箔运动方向不变,说明原子所带正电是均匀分布的 | |
| C. | α粒子轰击金箔实验现象说明原子的全部正电荷和几乎全部质量都集中在原子核里 | |
| D. | 卢瑟福通过α粒子轰击金箔的实验的数据记录估算出原子核的大小 |
2.关于重力做功和重力势能,下列说法正确的是( )
| A. | 重力做功与物体运动的路径有关 | |
| B. | 重力对物体做负功时,物体的重力势能一定减小 | |
| C. | 物体处在零势能面以下时,其重力势能为负值 | |
| D. | 重力势能的变化与零势能面的选取有关 |
19.下列关于卫星的说法正确的是( )(双选)
| A. | 周期是24h的卫星才有可能是同步卫星 | |
| B. | 同步卫星可以是可以通过两极 | |
| C. | 同步卫星的高度和线速度是定值 | |
| D. | 同步卫星的轨道是可以选择的 |