题目内容
6.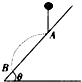 如图所示,小球由静止下落0.20m后与斜面上的A点碰撞弹起后又落到斜面上的B点.已知斜面与水平面的夹角θ=45°,g取1Om/s2,碰撞前后没有能量损耗.下列说法正确的是( )
如图所示,小球由静止下落0.20m后与斜面上的A点碰撞弹起后又落到斜面上的B点.已知斜面与水平面的夹角θ=45°,g取1Om/s2,碰撞前后没有能量损耗.下列说法正确的是( )| A. | 斜面上AB两点间的距离是1m | |
| B. | 小球落到斜面上B点时速度大小为6m/s | |
| C. | 小球做抛体运动的时间刚好是自由落体运动时间的2倍 | |
| D. | 小球落到斜面上B点时速度方向与水平方向夹角刚好为60° |
分析 根据自由落体运动的位移时间公式求出小球从起点运动到A点的时间.
小球与A点碰撞后做平抛运动,求出平抛运动的初速度,抓住平抛运动的水平位移和竖直位移相等求出平抛运动的时间,从而得出平抛运动到B点竖直方向上的分速度,根据平行四边形定则定则求出小球落到B点的速度大小.
解答 解:小球下降过程中,做自由落体运动,落到斜面A点的速度为v,
满足:2gh=v2
解得:$v=\sqrt{2gh}$=$\sqrt{2×10×0.2}=2$m/s
到达A点的时间:${t}_{1}=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.2}{10}}=0.2$s
小球从A到B做平抛运动,设A到B的时间为t2,
竖直方向:${x}_{AB}sinθ=\frac{1}{2}g{t}_{2}^{2}$
水平方向:xABcosθ=vt2
解得:t=0.4s
竖直方向的分速度:vy=gt2=10×0.4=4m/s
所以B点的速度为:${v}_{B}=\sqrt{{v}^{2}+{v}_{y}^{2}}=\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$m/s.
A、斜面上AB两点间的距离是:${x}_{AB}=\sqrt{2}v{t}_{2}=\sqrt{2}×2×0.4=0.8\sqrt{2}$m.故A错误;
B、由以上的计算可知,小球落到斜面上B点时速度大小为2$\sqrt{5}$m/s.故B错误;
C、由以上的计算可知,小球做抛体运动的时间是0.4s,刚好是自由落体运动时间0.2s的2倍.故C正确;
D、小球落到斜面上B点时速度方向与水平方向夹角:tanθ=$\frac{{v}_{y}}{v}=\frac{4}{2}=2$,所以θ≠60°.故D错误.
故选:C
点评 该题涉及两个过程,解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案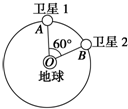 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.如图所示,“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置.若卫星均按顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.如图所示,“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置.若卫星均按顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )| A. | 这两颗卫星的速度大小相等,均为$\sqrt{\frac{r^2}{R}g}$ | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1中质量为m的物体的动能为$\frac{1}{2}$mgr | |
| D. | 卫星1由位置A运动到位置B所需的时间为$\frac{πr}{3R}$ $\sqrt{\frac{r}{g}}$ |
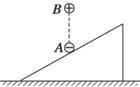 如图所示,可视为点电荷的小球 A、B分别带负电和正电,B球固定,其正下方的A球静止在绝缘斜面上,则( )
如图所示,可视为点电荷的小球 A、B分别带负电和正电,B球固定,其正下方的A球静止在绝缘斜面上,则( )| A. | A球一定受到2个力作用 | |
| B. | A球可能受到3个力作用 | |
| C. | A球受到的库仑力方向竖直向上 | |
| D. | A球在B球处产生的场强的方向竖直向上 |
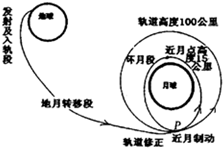 北京时间2013年12月2日,我国自行研制的“嫦娥三号”月球探测器在西昌卫星发射中心发射升空.图示是“嫦娥三号”飞行的轨道示意图,变轨过程是先从地月转移轨道经过修正进入环月圆轨道,然后再通过近月制动进入环月椭圆轨道,则以下说法正确的是( )
北京时间2013年12月2日,我国自行研制的“嫦娥三号”月球探测器在西昌卫星发射中心发射升空.图示是“嫦娥三号”飞行的轨道示意图,变轨过程是先从地月转移轨道经过修正进入环月圆轨道,然后再通过近月制动进入环月椭圆轨道,则以下说法正确的是( )| A. | “嫦娥三号”从地月转移轨道修正进入环月圆轨道过程中机械能守恒 | |
| B. | “嫦娥三号”在环月圆轨道和环月椭圆轨道上运行时,在切点P处的加速度a相同 | |
| C. | “嫦娥三号”在环月圆轨道上运行的周期比在环月椭圆轨道运行的周期大 | |
| D. | “嫦娥三号”近月制动完毕关闭发动机后,向近月点运行的过程中,势能减少,动能增加,机械能增加 |
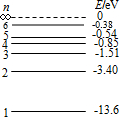 如图所示是氢原子的能级图,用光子能量为12.75eV的光照射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有( )
如图所示是氢原子的能级图,用光子能量为12.75eV的光照射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有( )| A. | 6种 | B. | 7种 | C. | 10种 | D. | 3种 |
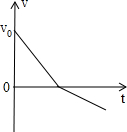 将一小球从地面以初速度v0竖直向上抛出,它运动的v-t图象如图所示,则小球( )
将一小球从地面以初速度v0竖直向上抛出,它运动的v-t图象如图所示,则小球( )| A. | 上升的最大高度为$\frac{{{v}_{0}}^{2}}{2g}$ | B. | 上升过程的加速度大于g | ||
| C. | 落回地面时的速度大小仍为v0 | D. | 上升过程比下降过程的平均速度大 |
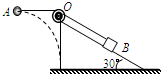 如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑轮O,倾角为30°的斜面体置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )
如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑轮O,倾角为30°的斜面体置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )| A. | 物块B受到的摩擦力一直增大 | |
| B. | 物块B受到的摩擦力先减小后增大 | |
| C. | 轻绳对B物体拉力先减小后增大 | |
| D. | 小球A的机械能不守恒,A、B系统的机械能守恒 |

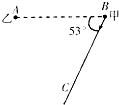 如图所示,A、B相距xAB=200m,∠ABC=53°.物体甲从B点以v=10m/s的速度向C运动,同时,物体乙从A点由静止开始做加速度a=5m/s2的匀加速直线运动.若要乙用最短时间到达BC线,取sin53°=0.8,cos53°=0.6,求乙到达BC线时与甲相距多远.
如图所示,A、B相距xAB=200m,∠ABC=53°.物体甲从B点以v=10m/s的速度向C运动,同时,物体乙从A点由静止开始做加速度a=5m/s2的匀加速直线运动.若要乙用最短时间到达BC线,取sin53°=0.8,cos53°=0.6,求乙到达BC线时与甲相距多远.