题目内容
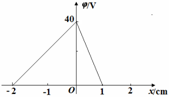 静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一带电微粒从x=-1cm的位置A由静止开始,在电场力作用下沿直线在A、B两点间往返运动,带电微粒质量m=1.0×10-20kg,带电量q=-1.0×10-9C,不计带电微粒的重力.求:
静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一带电微粒从x=-1cm的位置A由静止开始,在电场力作用下沿直线在A、B两点间往返运动,带电微粒质量m=1.0×10-20kg,带电量q=-1.0×10-9C,不计带电微粒的重力.求:(1)B点的位置坐标xB;
(2)带电微粒运动周期T.
分析:(1)根据图象求出电场强度的方向,应用动能定理求出距离B点的位置坐标xB;
(2)带电微粒在AB两点间先做匀加速运动,后做匀减速运动,应用牛顿第二定律与运动学公式可以求出粒子的运动时间,进一步可知周期T.
(2)带电微粒在AB两点间先做匀加速运动,后做匀减速运动,应用牛顿第二定律与运动学公式可以求出粒子的运动时间,进一步可知周期T.
解答:解:(1)由图知纵轴左右分别是匀强电场,
左侧电场沿-X方向,右侧电场沿+X方向,
大小分别为E1=
=2.0×103 N/C,E2=
=4.0×103N/C,
带电微粒由A运动到B的过程中,
由动能定理得:|q|?E1?|x|-|q|?E2?xB=0 ①,
由①式解得xB=
|x|=0.50cm ②;
(2)设微粒在虚线MN两侧的加速度大小分别为a1、a2,
由牛顿第二定律得:|q|E1=ma1 ③
|q|E2=ma2 ④
设微粒在虚线MN两侧运动的时间分别为t1、t2,
由运动学公式得:d1=
a1t12 ⑤d2=
a2t22 ⑥
从A点运动到B点的时间:t=t1+t2 ⑦
所以带电微粒运动周期T=2t
由②③④⑤⑥⑦式解得:T=3×10-8s;
答:(1)B点的位置坐标xB为0.50cm;(2)带电微粒运动周期T为3×10-8s.
左侧电场沿-X方向,右侧电场沿+X方向,
大小分别为E1=
| 40 |
| 0.02 |
| 40 |
| 0.01 |
带电微粒由A运动到B的过程中,
由动能定理得:|q|?E1?|x|-|q|?E2?xB=0 ①,
由①式解得xB=
| E1 |
| E2 |
(2)设微粒在虚线MN两侧的加速度大小分别为a1、a2,
由牛顿第二定律得:|q|E1=ma1 ③
|q|E2=ma2 ④
设微粒在虚线MN两侧运动的时间分别为t1、t2,
由运动学公式得:d1=
| 1 |
| 2 |
| 1 |
| 2 |
从A点运动到B点的时间:t=t1+t2 ⑦
所以带电微粒运动周期T=2t
由②③④⑤⑥⑦式解得:T=3×10-8s;
答:(1)B点的位置坐标xB为0.50cm;(2)带电微粒运动周期T为3×10-8s.
点评:根据图象判断出电场的方向、求出电场强度,应用动能定理与牛顿第二定律、运动学公式即可解题.

练习册系列答案
相关题目
 (2012?东城区二模)静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一质量为m、带电量为+q的粒子(不计重力),以初速度v0从O点进入电场,沿x轴正方向运动.下列叙述正确的是( )
(2012?东城区二模)静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一质量为m、带电量为+q的粒子(不计重力),以初速度v0从O点进入电场,沿x轴正方向运动.下列叙述正确的是( )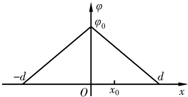 静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一带负电的粒子在电场中以x=0为中心、沿x轴方向在区间[-A,A]内做周期性运动,A<d.x0是x轴上的一点,x0<A.若图中φ0、d和A为已知量,且已知该粒子的比荷为
静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一带负电的粒子在电场中以x=0为中心、沿x轴方向在区间[-A,A]内做周期性运动,A<d.x0是x轴上的一点,x0<A.若图中φ0、d和A为已知量,且已知该粒子的比荷为| q |
| m |
| A、x=x0处的电场强度 |
| B、粒子经过x=x0时加速度的大小 |
| C、粒子经过x=x0时的动能与电势能之和 |
| D、粒子经过x=x0时速度的大小 |
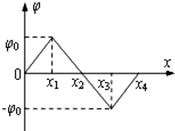 静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一质量为m、带电量为+q的粒子(不计重力),以初速度v0从O点(x=0)进入电场,沿x轴正方向运动.下列叙述正确的是( )
静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一质量为m、带电量为+q的粒子(不计重力),以初速度v0从O点(x=0)进入电场,沿x轴正方向运动.下列叙述正确的是( )| A、粒子从O运动到x1的过程中速度逐渐增大 | ||||||||
| B、粒子从x1运动到x3的过程中,电势能先减小后增大 | ||||||||
C、若v0=
| ||||||||
D、要使粒子能运动到x4处,粒子的初速度v0至少为
|
 (2011?北京)静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线,图中φ0和d为已知量.一个带负电的粒子在电场中以x=0为中心,沿x轴方向做周期性运动.已知该粒子质量为m、电量为-q,其动能与电势能之和为-A(0<A<qφ0).忽略重力.求:
(2011?北京)静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线,图中φ0和d为已知量.一个带负电的粒子在电场中以x=0为中心,沿x轴方向做周期性运动.已知该粒子质量为m、电量为-q,其动能与电势能之和为-A(0<A<qφ0).忽略重力.求: 静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.下列说法正确的是( )
静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.下列说法正确的是( )