题目内容
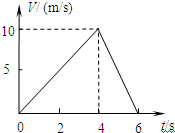 (2010?安徽)质量为2kg的物体在水平推力F的作用下沿水平面作直线运动,一段时间后撤去F,其运动的v-t图象如图.g取10m/s2,求:
(2010?安徽)质量为2kg的物体在水平推力F的作用下沿水平面作直线运动,一段时间后撤去F,其运动的v-t图象如图.g取10m/s2,求:(1)物体与水平面间的动摩擦因数μ;
(2)水平推力F的大小;
(3)在0~6s内物体运动平均速度的大小.
分析:(1)对减速运动,根据图象得到加速度,结合牛顿第二定律列式计算即可;
(2)求出加速过程的加速度,然后对加速过程运动牛顿第二定律列式分析即可;
(3)根据速度时间图象与时间轴包围的面积表示位移求解出总位移,再根据平均速度公式求解出平均速度的大小.
(2)求出加速过程的加速度,然后对加速过程运动牛顿第二定律列式分析即可;
(3)根据速度时间图象与时间轴包围的面积表示位移求解出总位移,再根据平均速度公式求解出平均速度的大小.
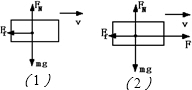
解答:解:(1)由题意可知:物体在4~6s内受力如图(1)所示,F合=Ff=μFN=μmg
由牛顿第二定律得物体的加速度a1=
=μg
又由v-t图象可知:物体在4~6s内加速度a1=
=5m/s2
所以μg=5m/s2,可得:μ=0.5
即物体与水平面间的动摩擦因数μ为0.5.
(2)由v-t图象可知:物体在0~4s内加速度:a2=
=2.5m/s2
又由题意可知:物体在0~4s内受力如图(2)所示,
F合=F-Ff=F-μmg=ma2
F=μmg+ma2,代入数据得:F=15N
即水平推力F的大小为15N.
(3)物体在0~6s内的位移大小在数值上为图象和时间轴包围的面积,
x=
×6×10m=30m
平均速度
=
=5m/s
即在0~6s内物体运动平均速度的大小为5m/s.

由牛顿第二定律得物体的加速度a1=
| F合 |
| m |
又由v-t图象可知:物体在4~6s内加速度a1=
| △v |
| t |
所以μg=5m/s2,可得:μ=0.5
即物体与水平面间的动摩擦因数μ为0.5.
(2)由v-t图象可知:物体在0~4s内加速度:a2=
| △v |
| t |
又由题意可知:物体在0~4s内受力如图(2)所示,
F合=F-Ff=F-μmg=ma2
F=μmg+ma2,代入数据得:F=15N
即水平推力F的大小为15N.
(3)物体在0~6s内的位移大小在数值上为图象和时间轴包围的面积,
x=
| 1 |
| 2 |
平均速度
. |
| v |
| x |
| t |
即在0~6s内物体运动平均速度的大小为5m/s.
点评:本题关键根据速度时间图象得到加速过程和减速过程的加速度,然后根据牛顿第二定律列式求解.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
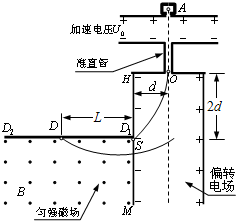 (2010?安徽模拟)如图所示的装置可测离子的比荷(荷质比).离子源A产生初速度可忽略不计的正离子,被电压为U0的加速电场加速后匀速通过准直管,然后从O点垂直射入匀强偏转电场,能正好从HM极板上的小孔S射出,立即进入垂直纸面向外的磁感应强度为B的匀强磁场区,最后打在水平放置的底片D1D2的D点(底片右端D1紧靠小孔S).已知HO=d,HS=2d,DS=L,忽略粒子所受重力.试求
(2010?安徽模拟)如图所示的装置可测离子的比荷(荷质比).离子源A产生初速度可忽略不计的正离子,被电压为U0的加速电场加速后匀速通过准直管,然后从O点垂直射入匀强偏转电场,能正好从HM极板上的小孔S射出,立即进入垂直纸面向外的磁感应强度为B的匀强磁场区,最后打在水平放置的底片D1D2的D点(底片右端D1紧靠小孔S).已知HO=d,HS=2d,DS=L,忽略粒子所受重力.试求