题目内容
3.如图所示,与水平方向成θ=37°的传送带以恒定速度v=4m/s沿逆时针方向转动,两传动轮间距为lAB=5.8m.一质量为M=1kg的长木板静止在粗糙地面上,其右端靠着传送带.现将一质量为m=1kg且可视为质点的物块轻放在传送带顶端B点,物块沿传送带滑至底端,正好滑上长木板(此过程无机械能损失).已知物块与传送带间的动摩擦因数为μ1=0.5,物块与长木板间的动摩擦因数为μ2=0.4,长木板与地面间的动摩擦因素为μ3=0.1,重力加速度g=10m/s2;求:
(1)物块刚滑到长木板上的速度大小
(2)从滑块滑上长木板到二者停下的总时间;
(3)为保证滑块不从长木板上滑下,长木板的最小长度.
分析 (1)根据牛顿第二定律可求得物体的加速度,再由运动学公式可求得物块刚滑到长木板上时的速度大小;
(2)分别对滑块和木板进行分析,根据牛顿第二定律求出各自的加速度;再由运动学公式明确达共同速度的时间;再对整体分析,由牛顿第二定律及运动学公式可求得停止的时间;
(3)根据运动学公式求得两小球达到共速时所经历的位移,再由位移公式求解各自的位移,即可明确最小长度.
解答 解:(1)物体轻放上传送带,根据牛顿第二定律可得:
mgsinθ+μ1mgcosθ=ma1
解得:a1=10m/s2;
物体以a1速至v2:
则有:v2=2a1l1
解得:l1=0.8m;
到达v之后以a2加速到B:
mgsinθ-μ1mgcosθ=ma2
解得:a2=2m/s2;
到达B速度为v0:
v20-v2=2a2(lAB-l1)
解得:v0=6m/s
(2)滑块滑上长木板,对滑块有:
μ2mg=ma3
解得:a3=4m/s2;
方向向右;
对长木板:μ2mg-μ3(m+M)g=Ma4
解得:a4=2m/s2;
方向向左;
二者速度相等经历的时间为t1:
则由速度公式可得:v0-a3t1=a4t1
解得:t1=1s;
速度为v1=2m/s;
共速后再共同匀减速,μ3(M+m)g=(M+m)a5
解得:a5=1m/s2
再到停下:t2=$\frac{{v}_{1}}{{a}_{5}}$=$\frac{2}{1}$=2s;
故总时间t=t1+t2=1+2=3s;
(3)达到共同速度时,滑块的位移x1=v0t1-$\frac{1}{2}{a}_{3}{t}_{1}^{2}$=6×1-$\frac{1}{2}×4×1$=4m;
木板的位移x2=$\frac{1}{2}{a}_{4}{t}_{1}^{2}$=$\frac{1}{2}×2×1$=1m;
故木板的长度至少为:x1-x2=4-1=3m;
答:
(1)物块刚滑到长木板上的速度大小为6m/s;
(2)从滑块滑上长木板到二者停下的总时间为3s;
(3)为保证滑块不从长木板上滑下,长木板的最小长度3m.
点评 本题考查牛顿第二定律的应用,涉及两个物体多个过程,要注意正确确定研究对象,做好受力分析,再根据牛顿第二定律结合运动学公式进行分析求解;注意掌握应用加速度的桥梁作用.

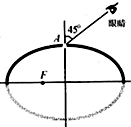 有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )| A. | $\frac{4}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
| A. | EA=EB | B. | EA<EB | ||
| C. | EA>EB | D. | EA、EB的大小不能确定 |

| A. | 重力和支持力的合力 | B. | 静摩擦力 | ||
| C. | 滑动摩擦力 | D. | 重力、支持力、牵引力的合力 |
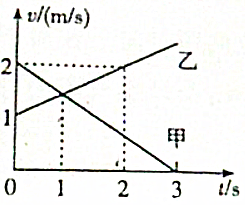 如图,是甲、乙两物体由同一位置开始做直线运动的v-t图象,下列表述正确的是( )
如图,是甲、乙两物体由同一位置开始做直线运动的v-t图象,下列表述正确的是( )| A. | 乙做匀加速直线运动,在第1s内与甲物体之间距离一直在减小 | |
| B. | 0~1s内甲和乙通过的位移相等 | |
| C. | 甲和乙的加速度方向相反,且甲的加速度大于乙的加速度 | |
| D. | 2s时甲、乙相遇 |
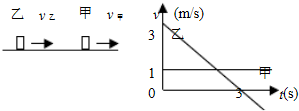 如图所示,甲乙两球前后相距1.5m,在两靠近的平行轨道上从同一方向作直线运动,它们的速度时间关系如图所示,则它们同时通过相同位移的时刻为( )
如图所示,甲乙两球前后相距1.5m,在两靠近的平行轨道上从同一方向作直线运动,它们的速度时间关系如图所示,则它们同时通过相同位移的时刻为( )| A. | 1s末 | B. | 2s末 | C. | 3s末 | D. | 4s末 |
| A. | 研究地球绕太阳公转时的地球 | |
| B. | 研究乒乓球运动员拉出的弧圈球 | |
| C. | 研究表演旋转动作的芭蕾舞演员 | |
| D. | 研究在双杠上表演动作的体操运动员 |
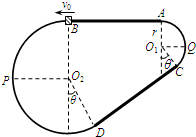 如图是放置在竖直平面内游戏滑轨的模拟装置的示意图.滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD的长度均为L=3m,圆弧形轨道AQC和BPD均光滑,AQC的半径为 r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角均为=37°.现有一质量为 m=1kg的滑块(可视为质点)穿在滑轨上,以v0=5m/s的初速度从B点开始水平向左运动,滑块与两段直轨道间的动摩擦因数均为μ=0.2,滑块经过轨道连接处的机械能损失忽略不计.取g=10m/s2,sin37°=0.6,求:
如图是放置在竖直平面内游戏滑轨的模拟装置的示意图.滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD的长度均为L=3m,圆弧形轨道AQC和BPD均光滑,AQC的半径为 r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角均为=37°.现有一质量为 m=1kg的滑块(可视为质点)穿在滑轨上,以v0=5m/s的初速度从B点开始水平向左运动,滑块与两段直轨道间的动摩擦因数均为μ=0.2,滑块经过轨道连接处的机械能损失忽略不计.取g=10m/s2,sin37°=0.6,求: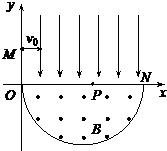 如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B,一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度V0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求
如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B,一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度V0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求