题目内容
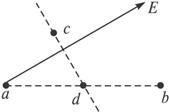
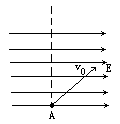
图中,a、b、c为匀强电场中的三等势面.b面的电势为零,且相邻等势面的电势差均相等.一带正电粒子从A点入射,其方向与水平成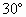 ,初动能
,初动能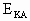 为16J,其在电场中最远可达到c面上的B点.试求:当该粒子动能为8J时,其电势能及运动速度方向.
为16J,其在电场中最远可达到c面上的B点.试求:当该粒子动能为8J时,其电势能及运动速度方向.
解析:
|
[解题过程]设粒子质量为m,初速度为 由于 依题意可知粒子运动至c面上的B点时,水平速度减小为零,即动能减少12J.由于整个过程中动能与电势能之和保持不变,故粒子由A→B,粒子(系统)电势能增加12J.依题意知b平面为零势面,且 当带电粒子动能
由于运动中粒子竖直方向速度始终不变,其动能 [思路点拨] 本题的求解关键有两个.①根据电场中电势能与动能之和守恒的关系求出总能量,进而确定此时的电势能.②根据运动规律可知:该粒子沿竖直方向运动速度不变,沿水平方向为匀速运动.若能求知由竖直方向运动所具有的动能,就可根据能量关系求出水平运动所具动能,进而求出运动方向. [小结] 用功能关系求解问题,是本章常用方法之一.特别是在非匀强电场中(例如带电粒子在点电荷场中的偏转),和运动过程较复杂的问题.例如,一带负电小球,如图所示进入匀强电场中,当其运动至最高点时速度大小与初速度大小相等.试判定最高点的位置应在A点的①正上方②左上方③右上方(重力作负功、电场力做正功、故应为左上方).用功能关系解题,主要指:动能定理和机械能与电势能的守恒关系.
|

 阅读快车系列答案
阅读快车系列答案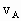 ,则
,则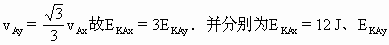 =4J.
=4J.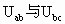 相等.故该粒子在a等势面的电势能为-6J(在c等势面的电势能为6 J),所以电势能与动能总和E等于10J(E=
相等.故该粒子在a等势面的电势能为-6J(在c等势面的电势能为6 J),所以电势能与动能总和E等于10J(E=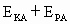 ).
).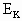 为8 J时,电势能
为8 J时,电势能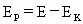 =10-8=2J.
=10-8=2J.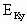 =4J也始终不变.所以当粒子动能为
=4J也始终不变.所以当粒子动能为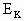 时,其水平运动所具动能
时,其水平运动所具动能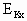 =4J.由此可知此时粒子运动方向应沿与水平方向成
=4J.由此可知此时粒子运动方向应沿与水平方向成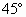 .
.
 电磁流量计广泛应用于测量可导电流体(如污水)在管中的流量(在单位时间内通过管内横截面的流体的体积).为了简化,假设流量计是如图所示的横截面为长方形的一段管道,长、宽、高分别为图中的a、b、c表示,左右两端开口,流量计的两端与输送流体的管道相连接.图中流量计的前后两面是金属材料,上下两面是绝缘材料.现于流量计所在处加竖直向下磁感应强度为B的匀强磁场,在管外将流量计前后两表面用导线串接一电阻R和电流表,当流体匀速流经流量计时,电流表读数为I.已知流体的电阻率为ρ,不计电流表的内阻,则流体的流量Q可表示为( )
电磁流量计广泛应用于测量可导电流体(如污水)在管中的流量(在单位时间内通过管内横截面的流体的体积).为了简化,假设流量计是如图所示的横截面为长方形的一段管道,长、宽、高分别为图中的a、b、c表示,左右两端开口,流量计的两端与输送流体的管道相连接.图中流量计的前后两面是金属材料,上下两面是绝缘材料.现于流量计所在处加竖直向下磁感应强度为B的匀强磁场,在管外将流量计前后两表面用导线串接一电阻R和电流表,当流体匀速流经流量计时,电流表读数为I.已知流体的电阻率为ρ,不计电流表的内阻,则流体的流量Q可表示为( )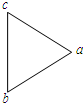 如图所示,a、b、c为匀强电场中的三点,这三点构成等边三角形,三角形的边长为30cm,若将一带电量q=-2×10-6C的点电荷从a点移到b点,电场力做的功W1=-1.2×10-5J;将同一点电荷从a点移到c点,电场力做的功W2=-6×10-6J,则将该点电荷从b点移到c点电场力做的功W3=
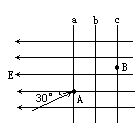
如图所示,a、b、c为匀强电场中的三点,这三点构成等边三角形,三角形的边长为30cm,若将一带电量q=-2×10-6C的点电荷从a点移到b点,电场力做的功W1=-1.2×10-5J;将同一点电荷从a点移到c点,电场力做的功W2=-6×10-6J,则将该点电荷从b点移到c点电场力做的功W3=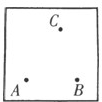 如图所示,方框中的A、B、C为匀强电场中的三个点,已知这三点的电势分别为φA=4V,φB=-1V,φC=2V,试在图中画出电势为2V的等势线及一条电场线.
如图所示,方框中的A、B、C为匀强电场中的三个点,已知这三点的电势分别为φA=4V,φB=-1V,φC=2V,试在图中画出电势为2V的等势线及一条电场线.