题目内容
（2003?顺德区模拟）如图所示，在X轴的上方（y≥0）存在着垂直于纸面向外的匀强磁场，磁感强度为B，在原点O有一个离子源向X轴上方的各个方向发射出质量为m，电量为q的正离子，速率都是V，对那些在xy平面内运动的离子，在磁场中可能达到的最大x=| 2mv |
| Bq |
| 2mv |
| Bq |
| πm |
| Bq |
| πm |
| Bq |
分析：由题意可知粒子的转动半径相同，由牛顿第二定律可求得粒子的转动半径；由几何关系可得出粒子能在x轴上能到达的最远距离．
解答：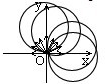
解：由洛伦兹力提供向心力得：
Bqv=m
解得：R=
沿-x轴方向射出的粒子圆心在y轴上，由图利用几何关系可知，所有粒子运动的圆心在以O为圆心，R为半径的圆中的第一象限部分，则可知，粒子在x轴上达到的最远距离为2R=
该离子从原点到x轴经过了半个周期，则t=
T=
×
=
故答案为：
；
解：由洛伦兹力提供向心力得：Bqv=m
| v2 |
| R |
解得：R=
| mv |
| Bq |
沿-x轴方向射出的粒子圆心在y轴上，由图利用几何关系可知，所有粒子运动的圆心在以O为圆心，R为半径的圆中的第一象限部分，则可知，粒子在x轴上达到的最远距离为2R=
| 2mv |
| Bq |
该离子从原点到x轴经过了半个周期，则t=
| 1 |
| 2 |
| 1 |
| 2 |
| 2πm |
| Bq |
| πm |
| Bq |
故答案为：
| 2mv |
| Bq |
| πm |
| Bq |
点评：本题解决的关键在于能通过分析找出所有粒子的运动轨迹间的关系，这种有无数粒子的问题要注意重点观测边界点的运动情况．
练习册系列答案
名校课堂系列答案
相关题目
（2003?顺德区模拟）如图所示，a为带正电的物体，b为不带电的绝缘物块，a、b叠放在粗糙水平地面上．地面上方有垂直纸面向里的匀强磁场，现用恒力F拉b，使a、b一起无相对滑动地向左加速运动，则在加速阶段，a受到b施加的摩擦力方向及大小变化是（ ）
（2003?顺德区模拟）角速度计可测量飞机、航天器、潜艇的转动角速度，其结构如图所示，当系统绕OO′转动时，元件A发生位移并输出的电压信号，成为飞机、卫星等的制导系统的信息源．已知A的质量为m，弹簧劲度系数为k、自然长度为L，电源电动势为E、内阻不计，滑动变阻器总长度为L．电阻分布均匀，系统静止时P在B点，当系统以角速度ω转动时，输出电压U和ω的函数式为
（2003?顺德区模拟）一个劲度系数为K=800N/m的轻弹簧，两端分别连接着质量均为m=12kg物体A和B，将它们竖直静止地放在水平地面上，如图所示．施加一竖直向上的变力F在物体A上，使物体A从静止开始向上做匀加速运动，当t=0.4s时物体B刚离开地面（设整个匀加速过程弹簧都处于弹性限度内，取g=10m/s2）．求：