题目内容
(4分)如图所示,在水平光滑直导轨上,静止着三个质量均为m=1kg的相同小球A、B、C,现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s,求A、B两球跟C球相碰前的速度和相碰后的速度。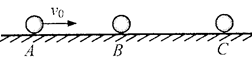
v1=1m/s,v2=0.5m/s
解析试题分析:设A、B两球跟C球相碰前、后的速度分别为v1、v2,对A、B两球相碰的过程,根据动量守恒定律有:mv0=2mv1,解得:v1=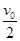 =1m/s
=1m/s
对A、B两球粘合在一起跟C球碰撞的过程,根据动量守恒定律有:2mv1=2mv2+mvC,解得:v2=v1-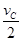 =0.5m/s
=0.5m/s
考点:本题主要考查了动量守恒定律的应用问题,属于中档偏低题。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
(1)在匀强磁场中,有一个原来静止的 C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为( )
C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为( )
A. C → C →  e+ e+ B B | B. C → C →  He+ He+ Be Be |
C. C → C →  H+ H+ B B | D. C → C →  e+ e+ N N |
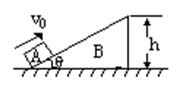
 ,一质量为
,一质量为 的小球,以速度
的小球,以速度 沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
下列四幅图的有关说法正确的是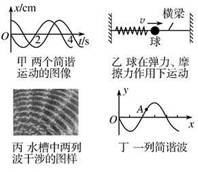
A.由图甲中两个简谐运动的图像可知,它们的相位差为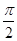 或者π 或者π |
| B.在图乙中,当球与横梁之间存在摩擦时,球的振动不是简谐运动 |
| C.由图丙可知,频率相同的两列波叠加时,某些区域的振动加强,某些区域的振动减弱 |
| D.如图丁所示,当简谐波向右传播时,质点A此时的速度沿y轴正方向 |
 )轰击轻金属铍(
)轰击轻金属铍( )时,发现有一种贯穿能力很强的中性射线.查德威克对该粒子进行研究,进而发现了新的粒子——中子.
)时,发现有一种贯穿能力很强的中性射线.查德威克对该粒子进行研究,进而发现了新的粒子——中子.
 ,匀强磁场的方向水平向外,磁感应强度为
,匀强磁场的方向水平向外,磁感应强度为 .有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为
.有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为 ,轨道半径为
,轨道半径为 .
.
 等于多少?
等于多少?

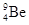 )得到中子的方程式.
)得到中子的方程式.