题目内容
【题目】如图所示．a、b、c 是地球大气层外圆形轨道上运动的三颗卫星，a 和 b 质量相等且小于 c 的质量，则（ ）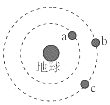
A.b 所需向心力最小
B.b、c 的周期相同且大于 a 的周期
C.b、c 的向心加速度大小相等，且大于 a 的向心加速度
D.c 加速可追上同一轨道上的 b，b 减速可等候同一轨道上的 c
【答案】A,B
【解析】解：A、三颗卫星均做匀速圆周运动，由万有引力提供向心力，则有 F=G 
，因为a、b质量相同，且小于c的质量，而b、c的轨道半径相等，且大于a的轨道半径，可知b所需向心力最小．故A正确；
B、卫星的周期公式为 T=2π 
，所以b、c的周期相同，且大于a的周期．故B正确；
C、向心加速度公式为 a= 
，可知b、c的向心加速度相等，且小于a的向心加速度，故C错误；
D、c加速后速度变大，所需要的向心力变大，c做离心运动，c的轨道半径变大，c不可能追上b；b减速后速度变小，所需要的向心力变小，b做向心运动，轨道半径变小，b不可能可等候同一轨道上的c，故D错误；
故选：AB
根据万有引力提供向心力，得出加速度、周期与轨道半径的大小关系，从而比较出大小．结合变轨原理分析．
练习册系列答案
相关题目
