题目内容
我国绕月探测工程的预先研究和工程实施已取得重要进展．设地球、月球的质量分别为m1、m2，半径分别为R1、R2，人造地球卫星的第一宇宙速度为v，对应的环绕周期为T，则环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为
v
v和
T
T．
|
|
|
|
分析：研究卫星绕地球运行和绕月球运行，根据万有引力充当向心力结合牛顿第二定律列出等式．
根据已知条件进行对比．
根据已知条件进行对比．
解答：解：卫星绕地球运行和绕月球运行都是由万有引力充当向心力，
根据牛顿第二定律有
=
=
得：v=
，
T=2π
所以有：
=
，
=
解得：v2=
v，T2=
T
即环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为
v，
T．
故答案为：
v，
T．
根据牛顿第二定律有
| GMm |
| R2 |
| mv2 |
| R |
| m?4π2R |
| T2 |
得：v=
|
T=2π
|
所以有：
| v2 |
| v |
| ||||
|
| T2 |
| T |
| ||||||
|
解得：v2=
|
|
即环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为
|
|
故答案为：
|
|
点评：求一个物理量之比，我们应该把这个物理量先用已知的物理量表示出来，再根据表达式进行比较．
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用．
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用．
练习册系列答案
英才计划期末调研系列答案
精英口算卡系列答案
相关题目
，
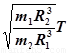B. 
，
，
D. 
，
，
B．
，