题目内容
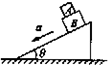 如图所示,A和B两物块又叠放在一起能够沿倾角为θ的斜面从静止开始共同加速滑下,已知A和B的质量分别为m和M,A和B之间的接触面与斜面平行,且动摩擦因数为μA,B与斜面间的动摩擦因数为μB,则下滑过程中,物体A受到摩擦力大小为
如图所示,A和B两物块又叠放在一起能够沿倾角为θ的斜面从静止开始共同加速滑下,已知A和B的质量分别为m和M,A和B之间的接触面与斜面平行,且动摩擦因数为μA,B与斜面间的动摩擦因数为μB,则下滑过程中,物体A受到摩擦力大小为分析:先对AB整体受力分析,根据牛顿第二定律求解出加速度,然后隔离出物体A,受力分析后根据牛顿第二定律列式求解出间的静摩擦力.
解答:解:先取AB为一整体,受力分析如图所示.
由牛顿第二定律得:(mA+mB)gsinθ-FfB=(mA+mB)a
FfB=μBFN
FN=(mA+mB)gcosθ
以上三式联立可得a=gsinθ-μBgcosθ
再隔离A物体,设A受到的静摩擦力为FfA,
方向沿斜面向上,对A再应用牛顿第二定律得:
mAgsinθ-FfA=mAa
可得出FfA=μBmAgcosθ.
故答案为:μBmAgcosθ
由牛顿第二定律得:(mA+mB)gsinθ-FfB=(mA+mB)a
FfB=μBFN
FN=(mA+mB)gcosθ
以上三式联立可得a=gsinθ-μBgcosθ
再隔离A物体,设A受到的静摩擦力为FfA,
方向沿斜面向上,对A再应用牛顿第二定律得:
mAgsinθ-FfA=mAa
可得出FfA=μBmAgcosθ.
故答案为:μBmAgcosθ
点评:本题关键是先对整体受力分析,根据牛顿第二定律求解出加速度,然后再隔离出物体P,运用牛顿第二定律求解PQ间的内力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,A和B两物块的接触面是水平的,A与B保持相对静止,并一起沿固定的光滑斜面向上运动,在向上运动的过程中,B受力个数为( ) 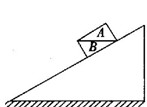
| A.3个 | B.4个 | C.5个 | D.6个 |
如图所示,A和B两物块的接触面是水平的,A与B保持相对静止一起沿固定斜面匀速下滑,在下滑过程中B的受力个数为( )
| A.3个 | B.4个 | C.5个 | D.6个 |
 (2011?大连模拟)如图所示,A和B两物块的接触面是水平的,A与B保持相对静止一起沿固定斜面匀速下滑,在下滑过程中B的受力个数为( )
(2011?大连模拟)如图所示,A和B两物块的接触面是水平的,A与B保持相对静止一起沿固定斜面匀速下滑,在下滑过程中B的受力个数为( )