题目内容
如图所示，固定斜面倾角为θ，整个斜面分为AB、BC两段，且2AB=BC．小物块P（可视为质点）与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2．已知P由静止开始从A点释放，恰好能滑动到C点而停下，则tanθ=分析：对物块进行受力分析，分析下滑过程中哪些力做功．
运用动能定理研究A点释放，恰好能滑动到C点而停下，列出等式找出答案．
运用动能定理研究A点释放，恰好能滑动到C点而停下，列出等式找出答案．
解答：解：A点释放，恰好能滑动到C点，物块受重力、支持力、滑动摩擦力．
设斜面AC长为L，
运用动能定理研究A点释放，恰好能滑动到C点而停下，列出等式：
mgLsinθ-μ1mgcosθ?
L-μ2mgcosθ?
L=0-0=0
解得：tanθ=
故答案为：tanθ=
设斜面AC长为L，
运用动能定理研究A点释放，恰好能滑动到C点而停下，列出等式：
mgLsinθ-μ1mgcosθ?
| 1 |
| 3 |
| 2 |
| 3 |
解得：tanθ=
| μ1+2μ2 |
| 3 |
故答案为：tanθ=
| μ1+2μ2 |
| 3 |
点评：了解研究对象的运动过程是解决问题的前提，根据题目已知条件和求解的物理量选择物理规律解决问题．要注意运动过程中力的变化．
练习册系列答案
名校课堂系列答案
相关题目
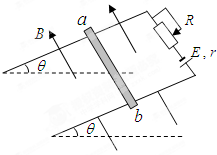
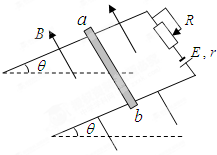如图所示，在倾θ=30°的绝缘斜面上，固定一L=0.25m的平行金属导轨，在导轨上端接入电源和滑动变阻器，电源电动E=12V，内r=1Ω，一质m=20g的金属ab与两导轨垂直并接触良好，整个装置处于磁感应强B=0.8T，方向垂直于斜面向上的匀强磁场中．金属导轨光滑，导轨与金属棒的电阻不计，g=10m/s2，要保持金属棒在导轨上静止，求：
如图所示，两个质量相等而粗糙程度不同的物体m1和m2，分别固定在一细棒的两端，放在一倾角为α的斜面上，设m1和m2与斜面的摩擦因数为μ1和μ2，并满足tanα=
