题目内容
6. 如图所示的正方形线框abcd边长为l,线圈水平放置,固定在磁感应强度为B,方向垂直的匀强磁场,其中ab边是电阻为R的匀强电阻丝,其余三边电阻不计,现有一段长度、粗细、材料均匀与ab边相同的电阻丝PQ架在线框上,并受到与ab平行的恒定水平力F作用从ad边由静止开始滑向bc边,PQ在滑动中与线框接触良好,摩擦阻力忽略不计,PQ电阻丝的质量为m,当PQ滑过$\frac{L}{3}$的距离时,它加速运动的加速度为a.
如图所示的正方形线框abcd边长为l,线圈水平放置,固定在磁感应强度为B,方向垂直的匀强磁场,其中ab边是电阻为R的匀强电阻丝,其余三边电阻不计,现有一段长度、粗细、材料均匀与ab边相同的电阻丝PQ架在线框上,并受到与ab平行的恒定水平力F作用从ad边由静止开始滑向bc边,PQ在滑动中与线框接触良好,摩擦阻力忽略不计,PQ电阻丝的质量为m,当PQ滑过$\frac{L}{3}$的距离时,它加速运动的加速度为a.(1)此时通过ap段电阻丝的电流为多少?
(2)从开始到此时过程中整个电路产生的焦耳热为多少?
分析 (1)据E=BLv求出感应电动势的大小,再通过闭合电路欧姆定律求出总电流,从而得出外电压,根据串并联电路的特点得出通过aP段电阻丝的电流强度的大小;
(2)根据牛顿运动定律知安培力大小,根据F=$\frac{{B}^{2}{L}^{2}v}{{R}_{总}}$知速度,根据动能定理知克服安培力做功,即整个电路产生的焦耳热.
解答 解:(1)PQ滑过$\frac{1}{3}$L的距离时,PQ产生的感应电动势的大小为:E=BLv.
整个电路的总电阻为:R总=R+$\frac{\frac{1}{3}R•\frac{2}{3}R}{\frac{1}{3}R+\frac{2}{3}R}$=$\frac{11}{9}$R
则干路中的电流为:I=$\frac{E}{{R}_{总}}$=$\frac{9BLv}{11R}$
aP、bP的电阻之比为1:2,则电流比为2:1,通过aP的电流大小为为:Iap=$\frac{2}{3}I$=$\frac{6BLv}{11R}$=$\frac{6(F-ma)}{11BL}$.
(2)根据牛顿运动定律知安培力F安=F-ma,
又F安=$\frac{{B}^{2}{L}^{2}v}{{R}_{总}}$
根据动能定理知F$•\frac{L}{3}$+W安=$\frac{1}{2}m{v}^{2}$-0
Q=-W安
解得Q=$\frac{1}{3}FL$$-\frac{121m{R}^{2}(F-ma)^{2}}{162{B}^{4}{L}^{4}}$
答:(1)通过ap段的电流大小为$\frac{6(F-ma)}{11BL}$.
(2)从开始到此时过程中整个电路产生的焦耳热为$\frac{1}{3}FL$$-\frac{121m{R}^{2}(F-ma)^{2}}{162{B}^{4}{L}^{4}}$.
点评 本题是电磁感应与电路的综合问题,关键画出等效电路,能求解总电阻,运用闭合电路欧姆定律进行求解.

| A. | 重力在上升过程的冲量大 | B. | 重力在上升过程的冲量小 | ||
| C. | 两过程中重力的冲量相等 | D. | 条件不足,不能确定 |
 一质量为m的物体以初速度v0竖直上抛,假如物体受到恒定的阻力,其v-t图象如图所示,t2时刻物体返回抛出点,下列说法正确的是 ( )
一质量为m的物体以初速度v0竖直上抛,假如物体受到恒定的阻力,其v-t图象如图所示,t2时刻物体返回抛出点,下列说法正确的是 ( )| A. | 末速度v1的大小等于初速度v0的大小 | |
| B. | 上升过程中的平均速度大于下降过程中的平均速度 | |
| C. | 物体受到的阻力为mg+$\frac{m{v}_{0}}{{t}_{1}}$ | |
| D. | 物体整个运动过程中均处于失重状态 |
| A. | 对一定质量的理想气体,温度越低,其内能越小 | |
| B. | 物体吸收热量的同时又对外做功,其内能可能增加 | |
| C. | 热力学第二定律可描述为“热量不可能由低温物体传递到高温物体” | |
| D. | 悬浮在液体中的微粒越大,在某一瞬间跟它相撞的液体分子就越多,布朗运动越明显 | |
| E. | 一定质量的气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加 |
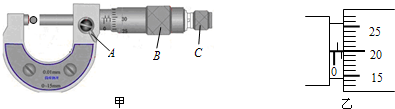
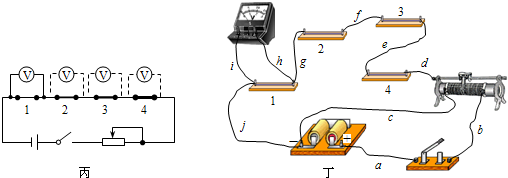 1.
1. 如图所示,一根长L=100cm、一端封闭的细玻璃管开口向上竖直放置,管内用h=25cm长的水银柱封闭了一段长L1=30cm的空气柱.已知大气压强为75cmHg,玻璃管周围环境温度为27℃.求:
如图所示,一根长L=100cm、一端封闭的细玻璃管开口向上竖直放置,管内用h=25cm长的水银柱封闭了一段长L1=30cm的空气柱.已知大气压强为75cmHg,玻璃管周围环境温度为27℃.求: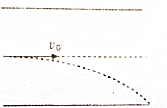 “理光牌”复印机的偏转电场如图所示,电容器的电容为C,板长为L,两极板间距为d,现有一个带电量为q,质量为m的墨粉微粒,以初速度v0沿两极板的中线垂直电场进入偏转电场中,若墨粉微粒恰能从极板边缘射出电场(不计重力),求:
“理光牌”复印机的偏转电场如图所示,电容器的电容为C,板长为L,两极板间距为d,现有一个带电量为q,质量为m的墨粉微粒,以初速度v0沿两极板的中线垂直电场进入偏转电场中,若墨粉微粒恰能从极板边缘射出电场(不计重力),求: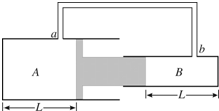 如图所示,“T”形活塞将绝热气缸内的气体分隔成A、B两部分,活塞左右两侧截面积分别为S1、S2,活塞至气缸两端底部的距离均为L,活塞与缸壁间无摩擦.气缸上a、b两个小孔用细管(容积不计)连通.初始时缸内气体的压强等于外界大气压强P0,温度为T0.现对缸内气体缓慢加热,发现活塞向右移动了△L的距离(活塞移动过程中不会经过小孔),求缸内气体的温度.
如图所示,“T”形活塞将绝热气缸内的气体分隔成A、B两部分,活塞左右两侧截面积分别为S1、S2,活塞至气缸两端底部的距离均为L,活塞与缸壁间无摩擦.气缸上a、b两个小孔用细管(容积不计)连通.初始时缸内气体的压强等于外界大气压强P0,温度为T0.现对缸内气体缓慢加热,发现活塞向右移动了△L的距离(活塞移动过程中不会经过小孔),求缸内气体的温度.