Question

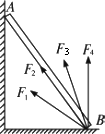
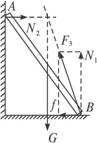
将二个正方形的光滑木板斜靠在竖直墙上，木板与水平地面的夹角分别为30°，45°和60°三种情况，将一个小球从木板顶端由静止开始释放，滑到小板底端的时间分别时t₁、t₂、t₃，则t₁、t₂、t₃的关系是

1. A.
   t₁＜t₂＜t₃
2. B.
   t₁＞t₂＞t₃
3. C.
   t₁=t₂=t₃
4. D.
   t₁=t₃＞t₂

Answer 1

B
分析：小球从木板顶端由静止开始释放，做初速度为零的匀加速直线运动；斜面倾角越大，下滑的加速度越大，根据位移时间关系公式列式分析即可．
解答：小球从木板顶端由静止开始释放，做初速度为零的匀加速直线运动，根据位移时间公式，有
x=
解得

斜面倾角越大，下滑的加速度越大，即
a₁＜a₂＜a₃
故
t₁＞t₂＞t₃
故选B．
点评：本题关键是发现小球的运动性质，然后根据位移时间公式列式分析；同时要明确斜面坡角越大，下滑的加速度越大．