题目内容
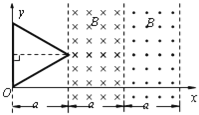
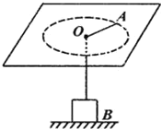
【题目】如图所示,在光滑的水平桌面上有一光滑小孔 0，一根轻绳穿过小孔，一端连接质量为 m=1kg的小球 A，另一端连接质量为 M=4kg的重物 B。求:
（1）当 A球沿半径为 R=0.1m的圆做匀速圆周运动,其角速度为ω=10rad/s时，B对地面的压力是多少?
（2）要使 B物体对地面恰好无压力，A球的角速度应为多大？（g=10m/s2）
【答案】（1）30N，方向竖直向下（2）20rad/s.
【解析】
（1）对小球A来说，小球受到的重力和支持力平衡．因此绳子的拉力提供向心力，则：FT=mRω2
解得：FT=10N
对物体B来说，物体受到三个力的作用：重力Mg、绳子的拉力FT、地面的支持力FN，
由力的平衡条件可得：FT+FN=Mg，故FN=Mg-FT
将FT=10N代入可得：FN=(4×10-10)N=30N
由牛顿第三定律可知，B对地面的压力为30N，方向竖直向下。
（2）当B对地面恰好无压力时，有：Mg=FT′，
拉力FT′提供小球A所需向心力，FT′=mRω′2
则有：ω′=20rad/s.
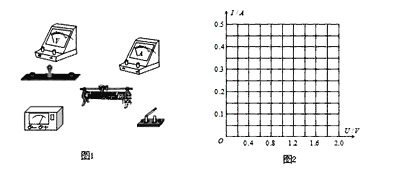
【题目】在描绘小灯泡的伏安特性曲线的实验中，小灯泡的额定电压为2.0V，额定电流约为0.5A，实验室提供下列实验器材．
电源E1：电动势为3.0V，内阻不计；
电源E2：电动势为12.0V，内阻不计；
电压表V：量程为0～3V，内阻约为10kΩ
电流表A1：量程为0～3A，内阻约为0.1Ω；
电流表A2：量程为0～0.6A，内阻约为0.6Ω；
滑动变阻器R：最大阻值为l0Ω，额定电流为1.0A；开关S，导线若干．
用实验得到如下数据（I和U分别表示小灯泡的电流和电压）：
I/A | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
U/V | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
（1）实验中电源应选用_________ ；电流表应选用 _________．
（2）将图1的实物连线成为实验电路______．
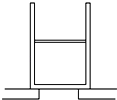
（3）在图2坐标中画出小灯泡的U﹣I曲线_______．
