Question

【题目】小船在200m宽的河中横渡，水流速度为2m/s，船在静水中的航速是4m/s，求：

(1)若小船的船头始终正对对岸行驶，它将在何时、何处到达对岸？

(2)要使小船到达河的正对岸，所用时间为多长？

(3)若水流速度是5m/s，船在静水中的速度是3m/s，则最短过河距离是多少？

Answer 1

【答案】(1)50s，下游100m；(2)s；(3)m

【解析】

(1)当小船的船头始终正对对岸时，渡河时间为

此过程船沿河流方向的位移为

s=v水t=2×50m=100m

所以船将历时50s时在河对岸的下游100m到达对岸。

(2)要使得小船到达正对岸，船在沿河岸方向上的合速度为零，即船的速度在沿河岸方向上的分量与水流的速度等大反向，设船在静水中的速度方向与河岸之间的夹角为θ，有：

v船cosθ=v水

代入数据解得θ=60°；到达对岸的时间为

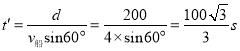
(3)若水流速度是5m/s，船在静水中的速度是3m/s，因水流的速度大于船在静水中的速度，所船不能垂直于河岸对河，要使渡河距离最小，需要使船在静水中的速度方向垂直于合速度的方向，此时合速度与河岸方向之间的夹角为θ′，有

得θ′=37°；此情况下渡河，船最短过河的距离为