题目内容

如图所示，一质量m1=0．45kg的平顶小车静止在光滑的水平轨道上。车顶右端放一质量m2 =0．4 kg的小物体，小物体可视为质点。现有一质量m0 =0．05 kg的子弹以水平速度v0 ="100" m/s射中小车左端，并留在车中，已知子弹与车相互作用时间极短，小物体与车间的动摩擦因数为=0．5，最终小物体以5 m/s的速度离开小车。g取10 m／s2。求：

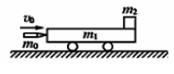
①子弹从射入小车到相对小车静止的过程中对小车的冲量大小。
②小车的长度。

①4.5N·s

解析试题分析：①子弹进入小车的过程中，子弹与小车组成的系统动量守恒，有：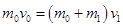
    2分
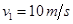可解得     1分
对子弹由动量定理有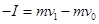：1分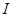
=4.5N·s(或Kgm/s)   1分
②三物体组成的系统动量守恒，由动量守恒定律有：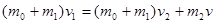
    2分
设小车长为L，由能量守恒有：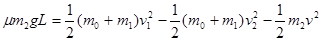
    2分
联立并代入数值得L＝5.5m    1分
考点：动量定理 动量守恒定律 能量守恒定律

练习册系列答案
相关题目

如图所示，半径为R的1/4光滑圆弧槽固定在小车上，有一小球静止在圆弧槽的最低点。小车和小球一起以速度v向右匀速运动。当小车遇到障碍物突然停止后，小球上升的高度可能是(      )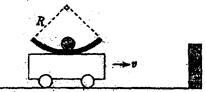

A．等于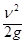 B．大于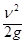
C．小于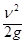 D．与小车的速度v无关

（4分）磁场具有能量，磁场中单位体积所具有的能量叫做能量密度，其值为B2/2μ,式中B是感应强度,μ是磁导率，在空气中μ为一已知常数．为了近似测得条形磁铁磁极端面附近的磁感应强度B，一学生用一根端面面积为A的条形磁铁吸住一相同面积的铁片P，再用力将铁片与磁铁拉开一段微小距离△L，并测出拉力F，如图所示．因为F所做的功等于间隙中磁场的能量，所以由此可得磁感应强度B与F、A之间的关系为B＝      

 

如图所示，水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ，它们的电阻可忽略不计，在M和P之间接有阻值为R="3.0Ω" 的定值电阻，导体棒ab长l=0.5m，质量m=1kg，其电阻为r=1.0Ω，与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中，磁感应强度B=0.4T.现使ab 以v0="10m/s" 的速度向右做匀速运动.

（1）使a、ｂ棒向右匀速的拉力F为多少？
（2）若撤掉拉力F，当导体棒速度v＝5m/s 时，试求导体棒的加速度大小为多少？
（3）试求从撤掉拉力F后，直至导体棒ab停止的过程中，在电阻R上消耗的焦耳热。

如图所示，质量mA＝2 kg的木块A静止在光滑水平面上．质量mB＝1 kg的木块B以初速度v0＝5 m/s向右运动，与A碰撞后两者均向右运动。木块A向右运动，与挡板碰撞反弹（与挡板碰撞无机械能损失)。后来与B发生二次碰撞，碰后A、B同向运动，速度大小分别为0.9 m/s、1.2 m/s。求：

（1）第一次A、B碰撞后A的速度；
（2）第二次碰撞过程中，A对B做的功。

（9分）两物块A、B用轻弹簧相连，质量均为2 kg，初始时弹簧处于原长，A、B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，质量4 kg的物块C静止在前方，如图所示。B与C碰撞后二者会粘在一起运动。求在以后的运动中：

（1）当弹簧的弹性势能最大时，物块A的速度为多大?
（2）系统中弹性势能的最大值是多少?

（10分）交流发电机转子有n匝线圈，每匝线圈所围面积为S，匀强磁场的磁感应强度为B，匀速转动的角速度为ω，线圈内电阻为r，外电路电阻为R。.当线圈由图中实线位置匀速转动90°到达虚线位置过程中，求：
（1）通过R的电荷量q为多少？
（2）R上产生的电热QR为多少？
（3）外力做的功W为多少？

如图16所示，两光滑轨道相距L=0.5m，固定在倾角为的斜面上，轨道下端连入阻值为R=4Ω的定值电阻，整个轨道处在竖直向上的匀强磁场中，磁感应强度B=1T，一质量m=0.1㎏的金属棒MN从轨道顶端由静止释放，沿轨道下滑，金属棒沿轨道下滑x=30m后恰达到最大速度（轨道足够长），在该过程中，始终能保持与轨道良好接触。（轨道及金属棒的电阻不计）

（1）金属棒下滑过程中,M、N哪端电势高.
（2）求金属棒下滑过程中的最大速度v.
（3）求该过程中回路中产生的焦耳热Q.

如图所示，小球从半径为2r的光滑圆弧形轨道的A点(A点与其圆心O在同一水平线上)由静止齐始下滑，滑至最低点D（切线呈水平状态）时进入半径为r，(且相接完好)的光滑半圆形轨道，则：

A．小球不能到达O处
B．小球能到O处，并且从O处开始做自由落体运动
C．小球由A点滑至D点后瞬间所受轨道支持力等于滑至D点前瞬间所受支持力
D．小球由A点滑至D点后瞬间的向心加速度小于滑至D点前瞬间的向心加速度

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网