��Ŀ����
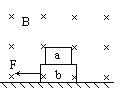
����Ŀ����ͼ��ʾ��ˮƽ�����뾶ΪR�İ�Բ�ι⻬��ֱ����������̶��ڵ����ϡ�����Ϊ�ʵ�Ļ���a ��С��b ������һ��ֹ�ڰ�ԲԲ�ĵ����·�N�㣬����a ��С��b�м����������ҩ��ijʱ�̵�ȼ��ҩ������a ��С��b˲����룬С��b ǡ����ͨ����Բ�������ߵ�P �㣬Ȼ����ƽ���˶��䵽ˮƽ���MN�ϡ���֪a ��b�����ֱ�Ϊ2m��m������a��ˮƽ���MN֮��Ķ�Ħ������Ϊ�����������ٶ�Ϊg����
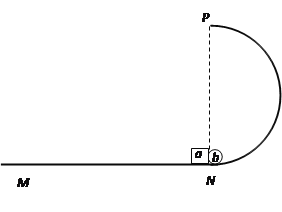
��1������a��С��b�շ���ʱb���ٶȴ�С��
��2��С��b����ص��뻬��a����ͣ�´�֮��ľ��롣
���𰸡���![]() ��
��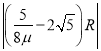
����������1������b����ֱƽ������Բ���˶�����P ��ʱ�����ṩ����������
![]()
���![]()
�������������b��Բ��������˶����ɶ��ܶ�����
![]()
���![]()
��2�� a��b ����˲����ˮƽ�����϶����غ㣬�ɶ����غ㶨����
mvb-2mva=0
���![]()
����a�����˶��ļ��ٶ�![]()
����a�����˶���������![]()
С��b��ƽ���˶�����ֱ������![]()
ˮƽ����Lb=vPt
���![]()
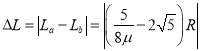

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ