题目内容
有人设想用图所示的装置来选择密度相同、大小不同的球状纳米粒子.粒子在电离室中电离后带正电,电量与其表面积成正比.电离后,粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II,其中磁场的磁感应强度大小为B,方向如图.收集室的小孔O3与O1、O2在同一条水平线上.半径为r0的粒子,其质量为m0、电量为q0,刚好能沿O1O3直线射入收集室.不计纳米粒子重力.(![]() )
)
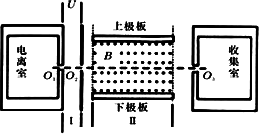
(1)试求图中区域II的电场强度;
(2)试求半径为r的粒子通过O2时的速率;
(3)讨论半径r≠r0的粒子刚进入区域II时向哪个极板偏转.
答案:
解析:
提示:
解析:
|
(1)设半径为r0的粒子加速后的速度为v0,则 设区域Ⅱ内电场强度为E,则 v0 q0B=q0E 电场强度方向竖直向上. (2)设半径为r的粒子的质量为m、带电量为q、被加速后的速度为v,则 由 (3)半径为r的粒子,在刚进入区域II时受到合力为: F合=qE-qvB=qB(v0-v) 由 r>r0时,v<v0,F合>0,粒子会向上极板偏转; r<r0时,v>v0,F合<0,粒子会向下极板偏转. |
提示:
|
本题考查带电在电磁场中的运动,综合考查了动能定理、受力分析等方面的知识和规律.对考生的分析综合能力、应用数学知识的能力要求较高 |

练习册系列答案
相关题目
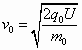
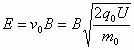
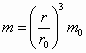
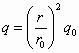
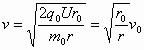


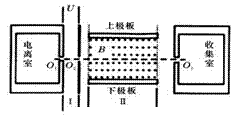 有人设想用图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电,电量与其表面积成正比。电离后,粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II,其中磁场的磁感应强度大小为B,方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子,其质量为m0、电量为q0,刚好能沿O1O3直线射入收集室。不计纳米粒子重力。(
有人设想用图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电,电量与其表面积成正比。电离后,粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II,其中磁场的磁感应强度大小为B,方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子,其质量为m0、电量为q0,刚好能沿O1O3直线射入收集室。不计纳米粒子重力。(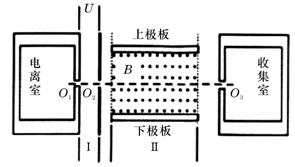
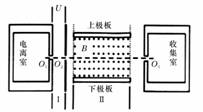 有人设想用图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电,电量与其表面积成正比。电离后,粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II,其中磁场的磁感应强度大小为B,方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子,其质量为m0、电量为q0,刚好能沿O1O3直线射入收集室。不计纳米粒子重力。
有人设想用图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电,电量与其表面积成正比。电离后,粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II,其中磁场的磁感应强度大小为B,方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子,其质量为m0、电量为q0,刚好能沿O1O3直线射入收集室。不计纳米粒子重力。