题目内容
4.某人造地球卫星绕地球做匀速圆周运动,它离地面的高度为地球半径R的3倍,已知地面附近的重力加速度为g,引力常量为G.求:(1)地球的质量;
(2)这颗人造地球卫星的向心加速度和周期.
分析 (1)在地面附近,物体的重力近似等于万有引力,由此列式,可求得地球的质量.
(2)人造地球卫星绕地球做匀速圆周运动,由万有引力提供卫星的向心力,由此列式,与上题的结果结合,即可求得结果.
解答 解:(1)设地球的质量为M,任一物体的质量为m′.在地球附近,有:
m′g=$\frac{GMm′}{{R}^{2}}$
解得:M=$\frac{g{R}^{2}}{G}$…①
(2)设人造地球卫星的质量为m,由万有引力提供卫星的向心力得:
G$\frac{Mm}{(4R)^{2}}$=ma=m$\frac{4{π}^{2}}{{T}^{2}}•4R$…②
由①②联立解得:a=$\frac{1}{16}$g,T=16π$\sqrt{\frac{R}{g}}$
答:(1)地球的质量是$\frac{g{R}^{2}}{G}$;
(2)这颗人造地球卫星的向心加速度是$\frac{1}{16}$g,周期是16π$\sqrt{\frac{R}{g}}$.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
14.在地球表面,用弹簧测力计测得质量为m0的物体的重力为P,已知地球的半径为R,万有引力常量为G,地球的同步通信卫星的轨道离地面的高度为h,则( )
| A. | 第一宇宙速度为v=$\sqrt{\frac{PR}{{m}_{0}}}$ | |
| B. | 地球的质量为$\frac{PR}{G{m}_{0}}$ | |
| C. | 地球的近地卫星环绕地球运动的向心加速度大小等于$\frac{P}{{m}_{0}}$ | |
| D. | 地球的自转周期等于$\frac{2π}{R}\sqrt{\frac{{m}_{0}(R+h)}{P}}$ |
15.加速器是使带电粒子获得高能量的装置,如图是回旋加速器的原理图,由回旋加速器的工作原理可知( )


| A. | 随着速度的增加,带电粒子在磁场中运动的周期越来越短 | |
| B. | 带电粒子获得的最大速度是由交变电场的加速电压决定的 | |
| C. | 加速质子后,不需要改变加速器的任何量,就可以用于加速α粒子 | |
| D. | 交变电场的频率跟带电粒子的比荷成正比 |
9.下列说法中正确的是( )
| A. | 电容器所带电荷量与两极板间的电势差成正比 | |
| B. | 根据动量定理可知,物体所受的合力与动量变化量成正比 | |
| C. | 电场中某点的电场强度与检验电荷在该点所受的电场力成正比 | |
| D. | 根据胡克定律可知,弹性限度内,弹簧的劲度系数与弹簧伸长量成正比 |
16.关于重力,下列说法中错误的是( )
| A. | 重力是物体的固有属性 | |
| B. | 重力的方向总是指向地心 | |
| C. | 重力的方向总是垂直向下 | |
| D. | 同一地点,物体受的重力跟物体的质量成正比 |
13.一物体自t=0时开始做直线运动,其速度-时间图象如图所示.下列选项正确的是( )
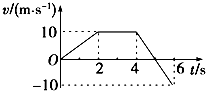

| A. | 在0~6s内,物体离出发点最远为30m | |
| B. | 在0~6s内,物体经过的路程为35m | |
| C. | 在0~4s内,物体的平均速度为7.5m/s | |
| D. | 在5~6s内,物体做匀减速直线运动 |
14.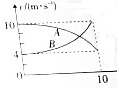 两个物块甲、乙在外力作用下沿同一方向做直线运动,它们的速度-时间图象分别如图所中实线A、B所示.在0~10s时间内,下列说法正确的是( )
两个物块甲、乙在外力作用下沿同一方向做直线运动,它们的速度-时间图象分别如图所中实线A、B所示.在0~10s时间内,下列说法正确的是( )
 两个物块甲、乙在外力作用下沿同一方向做直线运动,它们的速度-时间图象分别如图所中实线A、B所示.在0~10s时间内,下列说法正确的是( )
两个物块甲、乙在外力作用下沿同一方向做直线运动,它们的速度-时间图象分别如图所中实线A、B所示.在0~10s时间内,下列说法正确的是( )| A. | 甲的加速度逐渐减小,速度逐渐减小 | |
| B. | 乙的加速度逐渐增大,速度逐渐增大 | |
| C. | 甲、乙的位移均逐渐增大 | |
| D. | 甲、乙的平均速度大小均小于7m/s |



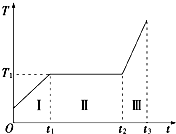 质量一定的某种物质,在压强不变的条件下,由液态Ⅰ到气态Ⅲ(可看成理想气体)变化过程中温度(T)随加热时间(t)变化关系如图所示.单位时间所吸收的热量可看作不变.
质量一定的某种物质,在压强不变的条件下,由液态Ⅰ到气态Ⅲ(可看成理想气体)变化过程中温度(T)随加热时间(t)变化关系如图所示.单位时间所吸收的热量可看作不变.