题目内容
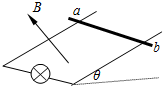（2011?宿迁三模）如图所示，光滑足够长导轨倾斜放置，导轨间距为L=1m，导轨平面与水平面夹角为θ=30°，其下端连接一个灯泡，灯泡电阻为R=3Ω，导体棒ab垂直于导轨放置，除灯泡外其它电阻不计．两导轨间的匀强磁场的磁感应强度为B=| 5 |
| 5 |
（1）导体棒的质量m；
（2）当导体棒速度为v=2.4m/s时，灯泡产生的热量Q；
（3）为了提高ab棒下滑到稳定状态时小灯泡的功率，试通过计算提出两条可行的措施．
分析：（1）根据导体棒下滑的位移x随时间t的变化关系x=3t-1.6，由数学知识可求出导体棒运动的最大速度，最大速度时，导体棒做匀速直线运动，重力沿斜面向下的分力与安培力平衡，由平衡条件可求出导体棒的质量．
（2）根据感应电量的公式q=
=
，可求出导体棒速度为v=2.4m/s时下滑的位移x，在这个过程中，导体棒的重力势能减小，转化为灯泡的内能和导体棒的动能，由能量守恒定律可求出灯泡产生的热量Q；
（3）根据功能关系得到灯泡功率的表达式，再从理论上分析提高ab棒下滑到稳定状态时小灯泡的功率的方法．
（2）根据感应电量的公式q=
| △Φ |
| R |
| BLx |
| R |
（3）根据功能关系得到灯泡功率的表达式，再从理论上分析提高ab棒下滑到稳定状态时小灯泡的功率的方法．
解答：解：（1）由题，导体棒的位移随时间变化关系趋近于x=3t-1.6，由数学知识得知，这是直线方程，其斜率大小等于速度，则得导体棒运动最大速度vm=3m/s．
此时导体棒做匀速直线运动，则有：mgsinθ=
代入数据化简得：m=1kg
（2）设导体棒下滑距离为x时速度为v=2.4m/s，在此过程中通过灯泡的电量：q=
，
根据能量守恒定律得：
mgxsinθ=Q+
mv2
代入数据化简得：Q=10.62J
（3）小灯泡的最大功率为：P=
此时又有：mgsinθ=
化简得：P=
因此，提高ab棒下滑到稳定状态时小灯泡的功率的措施有：增大导体棒的质量、增加导轨平面的倾角、换电阻较大的灯泡、减小磁场、减小导轨间距离．
答：（1）导体棒的质量m为1kg；
（2）当导体棒速度为v=2.4m/s时，灯泡产生的热量Q是10.62J；
（3）提高ab棒下滑到稳定状态时小灯泡的功率的措施有：增大导体棒的质量、增加导轨平面的倾角、换电阻较大的灯泡、减小磁场、减小导轨间距离．
此时导体棒做匀速直线运动，则有：mgsinθ=
| B2L2vm |
| R |
代入数据化简得：m=1kg
（2）设导体棒下滑距离为x时速度为v=2.4m/s，在此过程中通过灯泡的电量：q=
| BLx |
| R |
根据能量守恒定律得：
mgxsinθ=Q+
| 1 |
| 2 |
代入数据化简得：Q=10.62J
（3）小灯泡的最大功率为：P=
| (BLvm)2 |
| R |
| B2L2vm |
| R |
化简得：P=
| (mgsinθ)2R |
| B2L2 |
因此，提高ab棒下滑到稳定状态时小灯泡的功率的措施有：增大导体棒的质量、增加导轨平面的倾角、换电阻较大的灯泡、减小磁场、减小导轨间距离．
答：（1）导体棒的质量m为1kg；
（2）当导体棒速度为v=2.4m/s时，灯泡产生的热量Q是10.62J；
（3）提高ab棒下滑到稳定状态时小灯泡的功率的措施有：增大导体棒的质量、增加导轨平面的倾角、换电阻较大的灯泡、减小磁场、减小导轨间距离．
点评：本题的突破口是：位移的解析式x=3t-1.6，根据数学知识可求出导体棒的最大速度，同时，对导体棒的运动过程要会分析，而导体棒稳定时做匀速运动，可从力和能量两个角度研究．
练习册系列答案
阅读快车系列答案
相关题目
（2011?宿迁三模）如图所示电路中，L为电感线圈，C为电容器，当开关S由断开变为闭合时，则（ ）
（2011?宿迁三模）如图，一束质量、速度和电荷量不全相等的离子，沿同一直线经过由正交的匀强电场和匀强磁场组成的速度选择器后，进入另一个匀强磁场中分成A、B两束，下列说法正确的是（ ）
（2011?宿迁三模）甲乙两辆汽车同时从同一地点由静止出发沿同一直线运动，它们的速度图线如图示．下列说法正确的是（ ）
（2011?宿迁三模）在一种速降娱乐项目中，人乘坐在吊篮中，吊篮通过滑轮沿一条倾斜的钢索向下滑行．现有两条彼此平行的钢索，它们的起、终点分别位于同一高度．小红和小明分别乘吊篮从速降的起点由静止开始下滑，在他们下滑过程中，当吊篮与滑轮达到相对静止状态时，分别拍下一张照片，如图所示．已知二人运动过程中，空气阻力的影响可以忽略，则（ ）