��Ŀ����
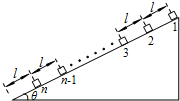 ��2012?������ģ�⣩��ͼ��ʾ���� n��n��10������ͬ��С��飨����Ϊ�ʵ㣩��ֹ�����Ϊ �� ����б����ϣ����������Ķ�Ħ��������Ϊ �̣�ÿ������������Ϊ m����������ľ����Ϊ l�����¶˵���鵽����˵ľ���ҲΪ l��ʹ��1�������ijһ���ٶ� v0�ع����ʼ�»�����ÿ�η�����ײʱ��鶼����ճ����һ���˶������n �����ճ��һ���ǡ��ͣ�ڹ���ĵˣ���֪���������ɺ��Բ��ƣ��������ٶ�Ϊg��
��2012?������ģ�⣩��ͼ��ʾ���� n��n��10������ͬ��С��飨����Ϊ�ʵ㣩��ֹ�����Ϊ �� ����б����ϣ����������Ķ�Ħ��������Ϊ �̣�ÿ������������Ϊ m����������ľ����Ϊ l�����¶˵���鵽����˵ľ���ҲΪ l��ʹ��1�������ijһ���ٶ� v0�ع����ʼ�»�����ÿ�η�����ײʱ��鶼����ճ����һ���˶������n �����ճ��һ���ǡ��ͣ�ڹ���ĵˣ���֪���������ɺ��Բ��ƣ��������ٶ�Ϊg����1�����һ����ײǰ˲��С���1���ٶ�v1�Ĵ�С��
��2�����5����ײǰ��˲���˶����Ķ���ΪEk5����5����ײ������ϵͳ��ʧ�Ļ�е��ΪE��5����E��5��Ek5�ı�ֵ��
��3�����»��������������������ײ����ʧ�Ļ�е�ܣ�
��������1���������1�»�l�Ĺ��̣��ɶ��ܶ�����ʽ�������v1�Ĵ�С��
��2�����5����ײǰ��5�����һ���˶����ٶȴ�СΪv5���Ե�5����ײ���ɶ����غ㶨����ʽ�����ݶ��ܵı���ʽд����ײǰ�˶����Ķ��ܣ����������ײ������ϵͳ��ʧ�Ļ�е�ܼ�����⣻
��3�����n��ľ���˶�����ײ��ȫ���������������ܹ��Ϳ˷�Ħ�������ܹ������������������仯�Ĺ�ϵ��ʽ������⣮
��2�����5����ײǰ��5�����һ���˶����ٶȴ�СΪv5���Ե�5����ײ���ɶ����غ㶨����ʽ�����ݶ��ܵı���ʽд����ײǰ�˶����Ķ��ܣ����������ײ������ϵͳ��ʧ�Ļ�е�ܼ�����⣻
��3�����n��ľ���˶�����ײ��ȫ���������������ܹ��Ϳ˷�Ħ�������ܹ������������������仯�Ĺ�ϵ��ʽ������⣮
����⣺��1���������1�»�l�Ĺ��̣��ɶ��ܶ�����mglsin��-��mglcos��=
m
-
m
�� v1=
��2�����5����ײǰ��5�����һ���˶����ٶȴ�СΪv5���Ե�5����ײ���ɶ����غ㶨���� 5mv5=��5m+m��v'5
��ײǰ�˶����Ķ���ΪEk5=
��5m
��ײ������ϵͳ��ʧ�Ļ�е��ΪE��5=
��5m
-
��6mv
���
=
��3����n��ľ���˶�����ײ��ȫ����
���������ܹ�WG=mglsin��(1+2+3+��+n)=
mglsin��
�˷�Ħ�������ܹ�Wf=��mgcos��?l(1+2+3+��+n)=
��mglcos��
�������������������ײ����ʧ�Ļ�е��ΪE����������������������仯�Ĺ�ϵ��WG+
mv02=Wf+E����
�����ϸ�ʽ��� E����=
mv02+
mgl(sin��-��cos��)
�𣺣�1����һ����ײǰ˲��С���1���ٶ�v1�Ĵ�СΪ
��
��2��E��5��Ek5�ı�ֵΪ
��
��3���»��������������������ײ����ʧ�Ļ�е��Ϊ
mv02+
mgl(sin��-��cos��)��
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
�� v1=
|
��2�����5����ײǰ��5�����һ���˶����ٶȴ�СΪv5���Ե�5����ײ���ɶ����غ㶨���� 5mv5=��5m+m��v'5
��ײǰ�˶����Ķ���ΪEk5=
| 1 |
| 2 |
| v | 2 5 |
��ײ������ϵͳ��ʧ�Ļ�е��ΪE��5=
| 1 |
| 2 |
| v | 2 5 |
| 1 |
| 2 |
| �� | 2 5 |
���
| E��5 |
| Ek5 |
| 1 |
| 6 |
��3����n��ľ���˶�����ײ��ȫ����
���������ܹ�WG=mglsin��(1+2+3+��+n)=
| n(n+1) |
| 2 |
�˷�Ħ�������ܹ�Wf=��mgcos��?l(1+2+3+��+n)=
| n(n+1) |
| 2 |
�������������������ײ����ʧ�Ļ�е��ΪE����������������������仯�Ĺ�ϵ��WG+
| 1 |
| 2 |
�����ϸ�ʽ��� E����=
| 1 |
| 2 |
| n(n+1) |
| 2 |
�𣺣�1����һ����ײǰ˲��С���1���ٶ�v1�Ĵ�СΪ
|
��2��E��5��Ek5�ı�ֵΪ
| 1 |
| 6 |
��3���»��������������������ײ����ʧ�Ļ�е��Ϊ
| 1 |
| 2 |
| n(n+1) |
| 2 |
������������Ҫ�����˶��ܶ����������غ㶨�ɼ����ܹ�ϵ��ֱ��Ӧ�ã����̽�Ϊ���ӣ��Ѷ����У�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
