题目内容
 (2011?杨浦区一模)如图所示,轻杆AC、AD长均为2m,轻杆AB长为3m,A端由活络头铰在一起,B、C、D均支于水平地面上,AB⊥AC,AB⊥AD,∠CAD=60°,在A端铰链上挂一重为G的物体,则AB杆所受压力的大小为
(2011?杨浦区一模)如图所示,轻杆AC、AD长均为2m,轻杆AB长为3m,A端由活络头铰在一起,B、C、D均支于水平地面上,AB⊥AC,AB⊥AD,∠CAD=60°,在A端铰链上挂一重为G的物体,则AB杆所受压力的大小为| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:先以A点为研究对象,分析受力,根据平衡条件求出AB杆对A的作用力和AD、AC杆对A点的合力大小,再运用分解法,求出AC对A点的作用力.
解答:解:设CD的中点为E.则AE=ACcos30°=
m.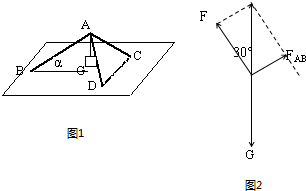
设AB杆与水平面的夹角为α,如图1,由数学知识得:tanα=
=
得,α=30°
以A点为研究对象,设AD、AC两杆对A点的作用力的合力为F,分析A点的受力如图2所示,由平衡条件得A与AB杆作用力的合力与重力G等值、反向,则由几何知识有:
F=Gcos30°=
G
FAB=Gsin30°=
G
设AC杆对A点的作用大小为FAC.由于AC=AD,由力的分解法得:
2FACcos30°=F
解得,FAC=
G
故由牛顿第三定律得知:AC杆所受压力的大小为
G.
故答案为:
G,
G
| 3 |

设AB杆与水平面的夹角为α,如图1,由数学知识得:tanα=
| AE |
| AB |
| ||
| 3 |
得,α=30°
以A点为研究对象,设AD、AC两杆对A点的作用力的合力为F,分析A点的受力如图2所示,由平衡条件得A与AB杆作用力的合力与重力G等值、反向,则由几何知识有:
F=Gcos30°=
| ||
| 2 |
FAB=Gsin30°=
| 1 |
| 2 |
设AC杆对A点的作用大小为FAC.由于AC=AD,由力的分解法得:
2FACcos30°=F
解得,FAC=
| 1 |
| 2 |
故由牛顿第三定律得知:AC杆所受压力的大小为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题中A点的受力分布在立体空间,分成两个平面进行分析,运用共点力平衡条件和分解法进行研究,中档难度.

练习册系列答案
相关题目
 (2011?杨浦区一模)一列简谐横波沿x轴传播,某时刻的波形如图所示,关于波的传播方向与质点a、b、c、d、e的运动情况.下列说法正确的是( )
(2011?杨浦区一模)一列简谐横波沿x轴传播,某时刻的波形如图所示,关于波的传播方向与质点a、b、c、d、e的运动情况.下列说法正确的是( ) (2011?杨浦区一模)调整如图所示电路的可变电阻R的阻值,使电压表V的示数增大△U,在这个过程中( )
(2011?杨浦区一模)调整如图所示电路的可变电阻R的阻值,使电压表V的示数增大△U,在这个过程中( ) (2011?杨浦区一模)如图所示,滑轮本身的质量可忽略不计,滑轮轴O安在一根轻木杆B上,一根轻绳AC绕过滑轮,A端固定在墙上,且绳保持水平,C端挂一重物,BO与竖直方向夹角θ=45°,系统保持平衡.若保持滑轮的位置不变,改变θ的大小,则滑轮受到木杆作用力大小变化情况是( )
(2011?杨浦区一模)如图所示,滑轮本身的质量可忽略不计,滑轮轴O安在一根轻木杆B上,一根轻绳AC绕过滑轮,A端固定在墙上,且绳保持水平,C端挂一重物,BO与竖直方向夹角θ=45°,系统保持平衡.若保持滑轮的位置不变,改变θ的大小,则滑轮受到木杆作用力大小变化情况是( )