题目内容

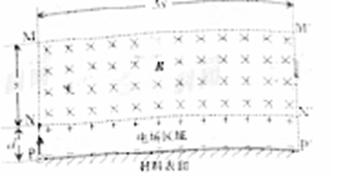
精英家教网某仪器用电场和磁场来控制电子在材料表面上方的运动．如图所示，材料表面上方矩形区域PP'N'N充满竖直向下的匀强电场，宽为d；矩形区域NN′M′M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN'为磁场与电场之间的薄隔离层．一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M'N'飞出．不计电子所受重力．
（1）求电子第二次与第一次圆周运动半径之比；
（2）求电场强度的取值范围；
（3）A是M′N′的中点，若要使电子在A、M′间垂直于AM′飞出，求电子在磁场区域中运动的时间．
分析：（1）电子会在两个区域内来回穿梭运动，在电场区域内做直线运动，在磁场区域内做圆周运动，且运动半径越来越小．应用能量关系和在磁场中的运动半径可知运动轨迹半径之比．
（2）电子不能从MM′边射出，从而确定了最大半径不能超过S，电子仅能从磁场边界M'N'飞出，电子所做的轨迹半径之和不小于3S，从这两个方面即可求出电场强度的范围．
（3）最终电子离开磁场时，运动半径应大于
S
2
，从而判断出能完成几个的半圆，最终时间是运动这几个半圆的时间再加上运动
1
4
圆周的时间．
解答：解：
（1）设圆周运动的半径分别为R1、R2、…Rn、Rn+1…，第一和第二次圆周运动速率分别为v1和v2，
动能分别为Ek1和Ek2
由：Ek2=0.81Ek1
R1=
mv1
Be
，R2=
mv2
Be

Ek1=
1
2
mv12，Ek2=
1
2
mv22
得：R2：R1=0.9：1
（2）设电场强度为E，第一次到达隔离层前的速率为v′，根据能量关系有：
eEd=
1
2
mv′2
0.9×
1
2
mv′2=
1
2
m
v
2
1

R1≤s
得：E≤
5B2es2
9md

又由：Rn=0.9n-1R1
2R1（1+0.9+0.92+…+0.9n+…）=3s
得：E＞
B2es2
80md

电场强度的取值范围为
B2es2
80md
＜E≤
5B2es2
9md

（3）设电子在匀强磁场中，圆周运动的周期为，运动的半圆周个数为n，运动总时间为t
由题意，有：
2R1(1-0.9n)
1-0.9
+Rn+1=3s
R1≤s
Rn+1=0.9nR1
Rn+1≥
s
2

得：n=2
由题意知，电子在磁场中做了2个半圆和一个
1
4
圆，
由：T=
2πm
eB

得：t=2×
1
2
T+
1
4
T=
5πm
2eB

答：（1）电子第二次与第一次圆周运动半径之比是0.9：1．
（2）电场强度的取值范围是
B2es2
80md
＜E≤
5B2es2
9md

（3）电子在磁场区域中运动的时间是
5πm
2eB
点评：当带电粒子在电磁场中做多过程运动、周期性运动、具有对称性的运动时，由于多种因素的影响，使问题形成多解．形成多解的原因一般包含以下几个方面：
（1）带电粒子电性不能确定形成多解．受洛伦兹力作用的带电粒子，可能带正电荷，也可能带负电荷，在相同的初速度下，正负离子在磁场中运动轨迹不同，导致形成双解．
（2）临界状态不唯一形成多解．带电粒子在洛伦兹力作用下飞越有界磁场时，由于粒子运动轨迹是圆弧状，因此，它可能穿过去，也可能转过1080从入射界面这边反向飞出．
（3）运动的重复性形成多解．带电粒子在磁场中运动时，由于某些因素的变化，例如磁场的强弱或方向做周期性变化或者速度方向突然反向等，运动具有重复性，因而形成多解．
练习册系列答案
相关题目

某仪器用电场和磁场来控制电子在材料表面上方的运动，如图所示，材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场，电场宽为d；矩形区域NN′M′M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN′为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，时间极短、运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M′N′飞出。不计电子所受重力。

（1）控制电子在材料表面上方运动，最大的电场强度为多少？
（2）若电子以上述最大电场加速，经多长时间将第三次穿越隔离层？
（3）A是M′N′的中点，若要使电子在A、M′间垂直于AM′飞出，求电子在磁场区域中运动的时间。

某仪器用电场和磁场来控制电子在材料表面上方的运动，如图所示，材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场，电场宽为d；矩形区域NN′M′M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN′为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，时间极短、运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M′N′飞出。不计电子所受重力。

（1）控制电子在材料表面上方运动，最大的电场强度为多少？
（2）若电子以上述最大电场加速，经多长时间将第三次穿越隔离层？
（3）A是M′N′的中点，若要使电子在A、M′间垂直于AM′飞出，求电子在磁场区域中运动的时间。

某仪器用电场和磁场来控制电子在材料表面上方的运动，如图所示，材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场，电场宽为d；矩形区域NN′M′M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN′为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，时间极短、运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M′N′飞出。不计电子所受重力。

（1）控制电子在材料表面上方运动，最大的电场强度为多少？

（2）若电子以上述最大电场加速，经多长时间将第三次穿越隔离层？

（3）A是M′N′的中点，若要使电子在A、M′间垂直于AM′飞出，求电子在磁场区域中运动的时间。

 

某仪器用电场和磁场来控制电子在材料表面上方的运动，如图所示，材料表面上方矩形区域PP'N'N充满竖直向下的匀强电场，宽为d；矩形区域NN'M'M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN'为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M'N'飞出。不计电子所受重力。

(1)求电子第二次与第一次圆周运动半径之比；

(2)求电场强度的取值范围；

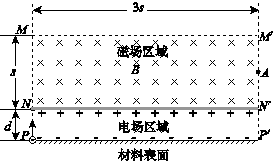
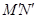(3)A是的中点，若要使电子在A、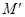间垂直于A飞出，求电子在磁场区域中运动的时间。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网