Question

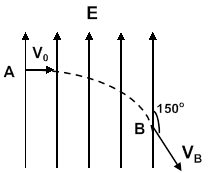
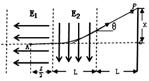
如图所示，虚线左侧有一场强为E₁=E的匀强电场，在两条平行的虚线MN和PQ之间存在着宽为L、电场强度为E₂=2E的匀强电场，在虚线PQ右侧相距也为L处有一与电场E₂平行的屏．现将一电子（电荷量e,质量为m）无初速度放入电场E₁中的A点，最后打在右侧的屏上，AO连线与屏垂直，垂足为O,求：

(1)电子从释放到打到屏上所用的时间；
(2)电子刚射出电场E₂时的速度方向与AO连线夹角的正切值tanθ；
(3) 电子打到屏上的点P到O点的距离x.

Answer 1

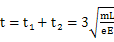(1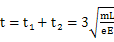) (2)2(3) x=3L

试题分析：(1)电子在电场E₁中初速度为零的匀加速直线运动，设加速度为a₁，时间t₁,由牛顿第二定律和运动学公式得：

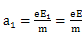
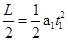       解得：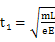                                         


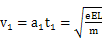
运动的总时间为：
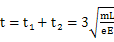
(2)设粒子射出电场E₂时沿平行电场线方向的速度为v_y，根据牛顿第二定律，粒子在电场中的加速度为：

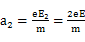
所以：

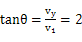
(3)设粒子在电场中的偏转距离为x，

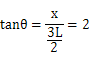
所以：x=3L。
点评：带电粒子在电场中的运动，综合了静电场和力学的知识，分析方法和力学的分析方法基本相同．先分析受力情况再分析运动状态和运动过程（平衡、加速、减速，直 线或曲线），然后选用恰当的规律解题．解决这类问题的基本方法有两种，第一种利用力和运动的观点，选用牛顿第二定律和运动学公式求解；第二种利用能量转化 的观点，选用动能定理和功能关系求解．