��Ŀ����
Ϊ�ˡ�̽�����ٶ������������Ĺ�ϵ�������ṩ��ͼ1��ʾʵ��װ�ã���˼��̽ ��˼·���ش�������˼��̽��˼·���ش��������⣺
��1��Ϊ������С����ˮƽľ�� ֮��Ħ������Ӱ��Ӧ��ȡ����
A�����������ֵ�ľ��һ�˵���ʵ���ʹС���ڹ���������ǡ���������˶���
B�����������ֵ�ľ��һ���ʵ���ߣ�ʹС���ڹ���������ǡ�����ȼ����˶���
C�����������ֵ�ľ��һ���ʵ���ߣ��ڲ��ҹ���������ʹС��ǡ���������˶���
D�����������ֵ�ľ��һ���ʵ���ߣ��ڲ��ҹ���������ʹС��ǡ�����ȼ����˶���
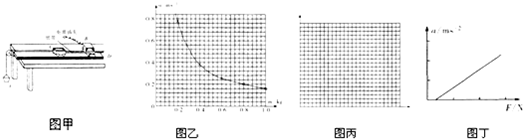
��2���ڡ�̽�����ٶ�������������ϵ����ʵ���У��õ�һ������ֽ������ͼ2��ʾ����֪���ڼ�������ʱ����ΪT���Ҽ��x1��x2��x3��x4��x5��x6����������С�����ٶȵı���ʽΪa=
��
��3������С����ˮƽľ��֮��Ħ������Ӱ����ù�������������С�����ܵ���������ʱ��������m��С��������M֮��Ӧ����Ĺ�ϵ

��1��Ϊ������С����ˮƽľ�� ֮��Ħ������Ӱ��Ӧ��ȡ����
C
C
��A�����������ֵ�ľ��һ�˵���ʵ���ʹС���ڹ���������ǡ���������˶���
B�����������ֵ�ľ��һ���ʵ���ߣ�ʹС���ڹ���������ǡ�����ȼ����˶���
C�����������ֵ�ľ��һ���ʵ���ߣ��ڲ��ҹ���������ʹС��ǡ���������˶���
D�����������ֵ�ľ��һ���ʵ���ߣ��ڲ��ҹ���������ʹС��ǡ�����ȼ����˶���
��2���ڡ�̽�����ٶ�������������ϵ����ʵ���У��õ�һ������ֽ������ͼ2��ʾ����֪���ڼ�������ʱ����ΪT���Ҽ��x1��x2��x3��x4��x5��x6����������С�����ٶȵı���ʽΪa=
| (x4+x5+x6)-(x1+x2+x3) |
| 9T2 |
| (x4+x5+x6)-(x1+x2+x3) |
| 9T2 |
��3������С����ˮƽľ��֮��Ħ������Ӱ����ù�������������С�����ܵ���������ʱ��������m��С��������M֮��Ӧ����Ĺ�ϵ
m����M
m����M
��
��������1��ƽ��Ħ����������С������������������������ֱ���˶�����������б��ķ�������С���ܵ���Ħ������
��2����ֽ��������ٶȿ���������⣮
��3��С���ܵ�������F����������������������������m��С��������M������F=
��ֻ�е�m����Mʱ��F�Ž��Ƶ���mg��
��2����ֽ��������ٶȿ���������⣮
��3��С���ܵ�������F����������������������������m��С��������M������F=
| Mmg |
| M+m |
����⣺��1��ƽ��Ħ����������С������������������������ֱ���˶�����������б��ķ�������С���ܵ���Ħ����������ƽ��ʱӦΪ�����������ֵ�ľ��һ���ʵ���ߣ��ڲ��ҹ���������ʹС��ǡ���������˶�����ѡ��C
��2�����ȱ����˶��Ĺ��ɵã�
x4-x1=3aT2
x5-x2=3aT2
x6-x3=3aT2
�����ã�
(x4+x5+x6)-(x1+x2+x3)=9aT2
��ã�a=
��3�������������m��С��������M������ٶ�Ϊa��
������F=Ma
�����mg-F=ma
�����ã�
F=
��ֻ�е�m����Mʱ���ſ��Ժ���m��F=
=mg
�ʴ�Ϊ����1��C����2��
����3��m����M
��2�����ȱ����˶��Ĺ��ɵã�
x4-x1=3aT2
x5-x2=3aT2
x6-x3=3aT2
�����ã�
(x4+x5+x6)-(x1+x2+x3)=9aT2
��ã�a=
| (x4+x5+x6)-(x1+x2+x3) |
| 9T2 |
��3�������������m��С��������M������ٶ�Ϊa��
������F=Ma
�����mg-F=ma
�����ã�
F=
| Mmg |
| M+m |
| Mmg |
| M |
�ʴ�Ϊ����1��C����2��
| (x4+x5+x6)-(x1+x2+x3) |
| 9T2 |
����������̽�����ٶ������������Ĺ�ϵ��ʵ��ʱ��ʵ�������ǰ�ƽ��Ħ������M����mҪ��ȷ����ֽ���������ٶȺ��ٶ��Ǹ���ʵ���г��õķ���һ��Ҫ�������գ�

��ϰ��ϵ�д�
�����Ŀ
 Ϊ��̽�����ٶ������Ĺ�ϵ��ʹ����ͼ��ʾ�����浼��װ�ý���ʵ�飮����G1��G2Ϊ��������ţ����������ּ�ʱ����������������ͨ��G1��G2�����ʱ���������ڵ���ʱ���t1����t2�����Ա���������¼����������ͬ����̶���һ���ε���Ƭ��������ΪM������Ƭ����ΪD������ż����Ϊx��ǣ�����������Ϊm��
Ϊ��̽�����ٶ������Ĺ�ϵ��ʹ����ͼ��ʾ�����浼��װ�ý���ʵ�飮����G1��G2Ϊ��������ţ����������ּ�ʱ����������������ͨ��G1��G2�����ʱ���������ڵ���ʱ���t1����t2�����Ա���������¼����������ͬ����̶���һ���ε���Ƭ��������ΪM������Ƭ����ΪD������ż����Ϊx��ǣ�����������Ϊm�� Ϊ��̽�����ٶ������Ĺ�ϵ��ʹ����ͼ��ʾ�����浼��װ�ý���ʵ�飮����G1��G2Ϊ��������ţ����������ּ�ʱ����������������ͨ��G1��G2�����ʱ���������ڵ���ʱ���t1����t2�����Ա���������¼����������ͬ����̶���һ���ε���Ƭ��������ΪM������Ƭ����ΪD������ż����Ϊx��ǣ�����������Ϊm���ش��������⣺
Ϊ��̽�����ٶ������Ĺ�ϵ��ʹ����ͼ��ʾ�����浼��װ�ý���ʵ�飮����G1��G2Ϊ��������ţ����������ּ�ʱ����������������ͨ��G1��G2�����ʱ���������ڵ���ʱ���t1����t2�����Ա���������¼����������ͬ����̶���һ���ε���Ƭ��������ΪM������Ƭ����ΪD������ż����Ϊx��ǣ�����������Ϊm���ش��������⣺