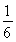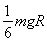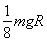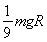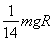题目内容
“嫦娥奔月”的过程可以简化为:质量为m的“嫦娥一号”升空后,绕地球沿椭圆轨道运动,然后经过变轨被月球捕获,再经多次变轨,最终绕月球做半径为r的匀速圆周运动.
(1)已知地球半径为R,表面的重力加速度为g,求“嫦娥一号”在距离地面h时受到地球的引力大小.
(2)已知月球的质量为M,引力常量为G,求“嫦娥一号”绕月球运动的周期T.
(1)已知地球半径为R,表面的重力加速度为g,求“嫦娥一号”在距离地面h时受到地球的引力大小.
(2)已知月球的质量为M,引力常量为G,求“嫦娥一号”绕月球运动的周期T.
分析:(1)由黄金代换和万有引力表达式可以得到引力大小
(2)由万有引力充当向心力的周期表达式,可以得到周期.
(2)由万有引力充当向心力的周期表达式,可以得到周期.
解答:解:(1)设地球质量为M1,对嫦娥一号有:
G
=mg
又:
F=G
解得:
F=
(2)
嫦娥一号绕月球运行时,有:
G
=m(
)2r
解得:
T=
答:
(1)已知地球半径为R,表面的重力加速度为g,“嫦娥一号”在距离地面h时受到地球的引力大小F=
(2)已知月球的质量为M,引力常量为G,求“嫦娥一号”绕月球运动的周期T=
G
| M1m |
| R2 |
又:
F=G
| M1m |
| (R+h)2 |
解得:
F=
| mgR2 |
| (R+h)2 |
(2)
嫦娥一号绕月球运行时,有:
G
| M1m |
| r2 |
| 2π |
| T |
解得:
T=
|
答:
(1)已知地球半径为R,表面的重力加速度为g,“嫦娥一号”在距离地面h时受到地球的引力大小F=
| mgR2 |
| (R+h)2 |
(2)已知月球的质量为M,引力常量为G,求“嫦娥一号”绕月球运动的周期T=
|
点评:易错点是运动的轨道半径,不是离地高度,而是离地高度加地球的半径,其次是要应用好黄金代换,题目给了地球半径和重力加速度,是明显的暗示.

练习册系列答案
相关题目
“嫦娥奔月”的过程可以简化为:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,在远地点时的速度为v,然后经过变轨被月球捕获,再经多次变轨,最终在距离月球表面高为h2="0.5" R2(R2为月球半径)的轨道上绕月球做匀速圆周运动.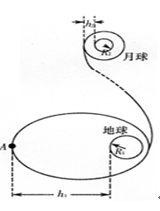
(1).已知地球半径为R1、表面的重力加速度为g0,求“嫦娥一号”沿椭圆轨道运动时在远地点A处的加速度a;(已知万有引力常量为G)
(2).飞船在距离月球表面高为h2="0.5" R2的轨道上绕行几圈后登陆月球,飞船上备有以下实验器材:
| A.计时表一只(测数据t) | B.弹簧测力计(测数据F) |
| C.已知质量为m的物体一个 | D.天平一只(附砝码一盒) |
①两次测量要选用的器材有________________ (用选项符号表示);
②两次测量的物理量是______________________和____________________;
③试用所给物理量的符号分别写出月球半径R2和质量M的表达式。