题目内容
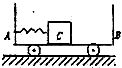 小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连接于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )
小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连接于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )分析:物体C与橡皮泥粘合的过程,系统机械能有损失;分析系统的合外力,即可判断动量是否守恒;根据动量守恒定律求解小车的速度.根据动量守恒定律求解AB向左运动的最大位移.
解答:解:A、物体C与橡皮泥粘合的过程,发生非弹簧碰撞,系统机械能有损失;故A错误.
B、整个系统在水平方向不受外力,竖直方向上合外力为零,则系统动量一直守恒,故B正确,
C、取物体C的速度方向为正方向,根据动量守恒定律得:0=mv+MV,得小车对地运动速度为V=-
v.故C错误.
D、当物体C与B端橡皮泥粘在一起时,系统又处于静止状态,此时AB车向左运动的位移最大,设最大位移为x,运动时间为t,
则根据动量守恒定律得:
m
-M
=0,得x=
.故D错误.
故选:B
B、整个系统在水平方向不受外力,竖直方向上合外力为零,则系统动量一直守恒,故B正确,
C、取物体C的速度方向为正方向,根据动量守恒定律得:0=mv+MV,得小车对地运动速度为V=-
| m |
| M |
D、当物体C与B端橡皮泥粘在一起时,系统又处于静止状态,此时AB车向左运动的位移最大,设最大位移为x,运动时间为t,
则根据动量守恒定律得:
m
| L-x |
| t |
| x |
| t |
| mL |
| m+M |
故选:B
点评:本题根据动量守恒和机械能守恒的条件进行判断:动量守恒的条件是系统不受外力或受到的外力的合力为零;机械能守恒的条件是除重力和弹力外的其余力不做功.

练习册系列答案
相关题目
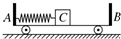 小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )
小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )| A、如果AB车内表面光滑,整个系统任何时刻机械能都守恒 | ||
| B、整个系统任何时刻动量都守恒 | ||
C、当木块对地运动速度为v时,小车对地运动速度为
| ||
| D、整个系统最后静止 |
 小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )
小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( ) 小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连接于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )
小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连接于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是( )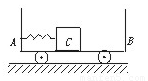
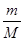 v
v