题目内容
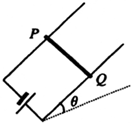 如图所示,两根无电阻导轨与水平面成θ=37°角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力fm=1.5N.当导轨间有竖直向上、磁感应强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求:
如图所示,两根无电阻导轨与水平面成θ=37°角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力fm=1.5N.当导轨间有竖直向上、磁感应强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求:(1)电源的电动势E.
(2)若将磁场改为垂直于导轨平面向下,要保证金属杆刚好不向下滑动,磁感应强度的大小不得超过多少?(g=10m/s2,sin37°=0.6,cos37°=0.8)
分析:(1)导体棒受重力、支持力、安培力处于平衡,根据共点力平衡求出电源的电动势.
(2)导体棒受重力、支持力、安培力,摩擦力处于平衡,根据共点力平衡求出磁感应强度的大小.
(2)导体棒受重力、支持力、安培力,摩擦力处于平衡,根据共点力平衡求出磁感应强度的大小.
解答: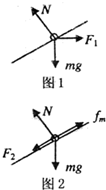 解:(1)棒在三个力作用下平衡,其中安培力F1方向水平向右(如图1所示).
解:(1)棒在三个力作用下平衡,其中安培力F1方向水平向右(如图1所示).
且安培力大小F1=BId
由平衡条件得F1cos37°=mg sin37°
回路中电流I=
=
=1.5A
电源的电动势E=I(R+r)=1.5×(4+1)=7.5V
(2)棒刚好不下滑时,受力如图2所示.
其中安培力F2=BmId
由平衡条件得BmId+mgsin 37°=fm
Bm=
=
T=
T=0.4T.
答:(1)电源的电动势E为7.5V;
(2)磁感应强度的大小不得超过0.4T.
 解:(1)棒在三个力作用下平衡,其中安培力F1方向水平向右(如图1所示).
解:(1)棒在三个力作用下平衡,其中安培力F1方向水平向右(如图1所示).且安培力大小F1=BId
由平衡条件得F1cos37°=mg sin37°
回路中电流I=
| mgsin37° |
| Bdcos37° |
| 0.2×10×0.6 |
| 2×0.5×0.8 |
电源的电动势E=I(R+r)=1.5×(4+1)=7.5V
(2)棒刚好不下滑时,受力如图2所示.
其中安培力F2=BmId
由平衡条件得BmId+mgsin 37°=fm
Bm=
| fm-mgsin37° |
| Id |
| 1.5-0.2×10×0.6 |
| 1.5×0.5 |
| 0.3 |
| 0.75 |
答:(1)电源的电动势E为7.5V;
(2)磁感应强度的大小不得超过0.4T.
点评:解决本题的关键掌握闭合电路欧姆定律,安培力的大小公式,以及会利用共点力平衡去求未知力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
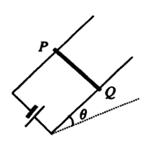
 角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力
角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力 N.当导轨间有竖直向上、磁感应强度为B=2
N.当导轨间有竖直向上、磁感应强度为B=2 T的匀强磁场时,杆与导轨间刚好无摩擦力.求:
T的匀强磁场时,杆与导轨间刚好无摩擦力.求:
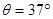 角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力
角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力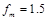 N.当导轨间有竖直向上、磁感应强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求:
N.当导轨间有竖直向上、磁感应强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求: