题目内容
10. 如图所示,传送带以一定速度沿水平方向匀速运动,将质量m=1.0kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧的两端点,其连线水平,轨道最低点为O,已知圆弧对应圆心角θ=106°,圆弧半径R=1.0m,A点距水平面的高度h=0.8m,小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动,经过 0.8s小物块 第二次经过D点,已知小物块与斜面间的动摩擦因数μ=$\frac{1}{3}$.(取sin53°=0.8,g=10m/s2)求:
如图所示,传送带以一定速度沿水平方向匀速运动,将质量m=1.0kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧的两端点,其连线水平,轨道最低点为O,已知圆弧对应圆心角θ=106°,圆弧半径R=1.0m,A点距水平面的高度h=0.8m,小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动,经过 0.8s小物块 第二次经过D点,已知小物块与斜面间的动摩擦因数μ=$\frac{1}{3}$.(取sin53°=0.8,g=10m/s2)求:(1)小物块离开A点时的水平速度大小;
(2)小物块经过O点时,轨道对它的支持力大小;
(3)斜面上C、D间的距离.
分析 (1)小物块离开A点后做平抛运动,根据经过B点的速度方向与竖直下落高度,求A点水平初速μ<度的大小;
(2)由动能定理求出物块经过O点的速度,根据牛顿第二定律求解轨道对小物块的支持力;
(3)根据牛顿第二定律求出物块在斜面上运动的加速度,由运动学公式求解C、D间的距离.
解答 解:(1)对于小物块,由A到B做平抛运动,在竖直方向上有
vy2=2gh ①
在B点时有tan$\frac{θ}{2}$=$\frac{{v}_{y}}{{v}_{A}}$ ②
由①②解得 vA=3m/s
(2)小物块在B点的速度为 vB=$\sqrt{{v}_{A}^{2}+{v}_{y}^{2}}$=5m/s
由B到O由动能定理(或机械能守恒定律)得
mgR(1-sin37°)=$\frac{1}{2}$mvO2-$\frac{1}{2}$mvB2;
由牛顿第二定律得 FN-mg=m$\frac{{v}_{O}^{2}}{R}$
解得FN=43N
(3)物块沿斜面上滑时,有 mgsin53°+μmgcos53°=ma1
vC=vB=5m/s
小物块由C上升到最高点的时间为 t1=$\frac{{v}_{C}}{{a}_{1}}$=0.5s
则小物块由斜面最高点回到D点历时
t2=0.8s-0.5s=0.3s
小物块沿斜面下滑时,由牛顿第二定律得
mgsin53°-μmgcos53°=ma2
C、D间的距离为 xCD=$\frac{{v}_{C}}{2}$t1-$\frac{1}{2}$a2t2=0.98m.
答:
(1)小物块离开A点时的水平速度大小为3m/s.
(2)小物块经过O点时,轨道对它的支持力大小为43N.
(3)斜面上C、D间的距离是0.98m.
点评 本题是平抛运动与圆周运动及动力学问题的综合,解决问题的关键是掌握相关基础知识,分过程处理.

 阅读快车系列答案
阅读快车系列答案| A. | c=$\frac{λ}{f}$ | B. | c=$\frac{f}{λ}$ | C. | c=λf | D. | c=$\sqrt{λf}$ |
| A. | 自然界存在两种电荷:正电荷与负电荷 | |
| B. | 正电荷吸引正电荷,负电荷吸引负电荷 | |
| C. | 同种电荷相互排斥 | |
| D. | 异种电荷相互排斥 |
 质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的动摩擦因数均为μ,系统在水平拉力F作用下匀速向右运动,选水平向右为正方向,如图所示.如突然撤消拉力F,则刚撤消后瞬间,二者的加速度aA和aB分别为( )
质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的动摩擦因数均为μ,系统在水平拉力F作用下匀速向右运动,选水平向右为正方向,如图所示.如突然撤消拉力F,则刚撤消后瞬间,二者的加速度aA和aB分别为( )| A. | aA=0,aB=0 | B. | aA>0,aB<0 | C. | aA<0,aB>0 | D. | aA<0,aB=0 |
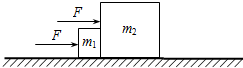 如图所示,两相互接触的物块放在光滑的水平面上,质量分别为m1和m2,且有m1<m2.现对两物块同时施加相同的水平恒力F.设在运动程中两物块之间的相互作用力大小为FN,则( )
如图所示,两相互接触的物块放在光滑的水平面上,质量分别为m1和m2,且有m1<m2.现对两物块同时施加相同的水平恒力F.设在运动程中两物块之间的相互作用力大小为FN,则( )| A. | FN=0 | B. | FN>2F | C. | 0<FN<F | D. | F<FN<2F |
 如图所示,飞船沿半径为R的圆周绕地球运动,其周期为T,地球半径为R0,若飞船要返回地面,可在轨道上某点A处将速率降到适当的数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切,求飞船由A点到B点所需要的时间.
如图所示,飞船沿半径为R的圆周绕地球运动,其周期为T,地球半径为R0,若飞船要返回地面,可在轨道上某点A处将速率降到适当的数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切,求飞船由A点到B点所需要的时间.



 如图甲所示,一对平行轨道固定放置在水平面上,两轨道间距为L.电阻为R0有一个质量为m的导体杆静止地放在轨道上,与两轨道垂直.杆及轨道的电阻皆可忽略不计.整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于轨道面.现用一外力F沿轨道方向拉杆,使之做匀加速运动,测得拉力F与时间t的关系如图乙所示,其中直线的斜率k=$\frac{g{B}^{2}{L}^{2}}{R}$,g为重力加速度.在T时刻将拉力撤去,杆从撤力开始,经过时间$\frac{T}{3}$停止运动.求:
如图甲所示,一对平行轨道固定放置在水平面上,两轨道间距为L.电阻为R0有一个质量为m的导体杆静止地放在轨道上,与两轨道垂直.杆及轨道的电阻皆可忽略不计.整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于轨道面.现用一外力F沿轨道方向拉杆,使之做匀加速运动,测得拉力F与时间t的关系如图乙所示,其中直线的斜率k=$\frac{g{B}^{2}{L}^{2}}{R}$,g为重力加速度.在T时刻将拉力撤去,杆从撤力开始,经过时间$\frac{T}{3}$停止运动.求: