��Ŀ����
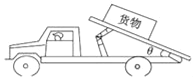
����Ŀ����ͼ��ʾ��һСľ�����ƽ�峵���в�����ƽ�峵�ĺ�ˡ���ʻ�Һ�˾�ΪL=2.0m�����ھ�ֹ״̬��ľ����ƽ�峵֮��Ķ�Ħ��������=0.40����ʹƽ�峵��ˮƽ·�����Լ��ٶ�a0�ȼ����������ٶȴﵽv=6.0m/s�����������ֱ���˶����˶�һ��ʱ����ȼ���ɲ���������Ħ�������ڻ���Ħ������ȡg=10m/s2��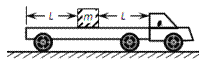
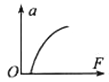
��1����ľ����ƽ�峵������Ծ�ֹ�����ٶ�a0��С����ʲô������
��2����a0=6.0m/s2����ľ����ƽ�峵���ٶȶ��ﵽ6.0m/sʱ����ľ����ƽ�峵�����ʻ�Һ�˾���s��
��3������ľ���ٶȸմﵽ6.0m/sʱƽ�峵�����ú㶨������ɲ����Ҫʹľ�䲻��ײ����ʻ�ң�ƽ�峵ɲ��ʱ�ļ��ٶȴ�СaӦ����ʲô������
���𰸡���1��![]() ��2��3.5m��3��
��2��3.5m��3��![]()
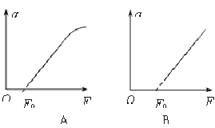
����������1��ľ���복��Ծ�ֹ�����ٶ���ͬ�������ֵΪam����ţ�ٵڶ�������
![]()
��� ![]()
��Ӧ���������Ϊ ![]()
��2������![]() ����ľ���복������Ի���
����ľ���복������Ի���
ľ���ٶȴﵽv=6m/s�����ʱ�� ![]()
�˶���λ�� ![]()
ƽ�峵�ٶȴﵽv=6m/s�����ʱ�� ![]()
�˶���λ�� ![]()
���� ![]()
��� ![]()
��3��ľ�����ֹͣʱ��λ�� ![]()
ƽ�峵����ֹͣʱ��λ�� ![]()
ľ�䲻�복����Ӧ���� ![]()
��� ![]()

��ϰ��ϵ�д�
�����Ŀ