题目内容
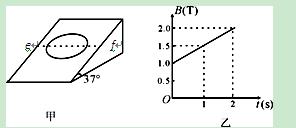
如图甲所示,在一倾角为37°的粗糙绝缘斜面上,静止地放置着一个匝数n=10匝的圆形线圈,其总电阻R=3.14Ω、总质量m=0.4kg、半径r=0.4m.向下轻推一下线圈恰能使它沿斜面匀速下滑。现在将线圈静止放在斜面上后,在水平直线ef(与线圈的水平直径重合)以下的区域中,加上垂直斜面方向、磁感应强度大小按如图乙所示规律变化的磁场,求:
(1)刚加上磁场时线圈中的感应电流大小I;
(2)从加上磁场开始到线圈刚要运动,线圈中产生的热量Q。(最大静摩擦力等于滑动摩擦力,sin37°=0.6,cos37°=0.8,g=10m/s2)
(1)I=0.4(A)
(2)Q=0.5(J) (3分)
。
解析:解:(1)由闭合电路欧姆定律得:
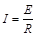 ① (2分)
① (2分)
由法拉第电磁感应定律得:
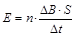 ② (2分)
② (2分)
由题意及图有:
 ③ (1分)
③ (1分)
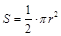 ④ (1分)
④ (1分)
联解①②③④得:I=0.4(A) (2分)
(2)设线圈开始能匀速滑动时受的滑动摩擦力为Fμ,则:
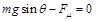 ⑤ (2分)
⑤ (2分)
加变化磁场后,线圈刚要运动时有:
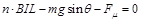 ⑥ (2分)
⑥ (2分)
由题意和图像得:
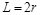 ⑦ (1分)
⑦ (1分)
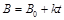 ⑧ (1分)
⑧ (1分)
由焦耳定律得:
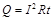 ⑨ (2分)
⑨ (2分)
联解①②③④⑤⑥⑦⑧⑨得:Q=0.5(J) (3分)
注:若有其他合理解法且答案正确,可同样给分。

 阅读快车系列答案
阅读快车系列答案