题目内容
17.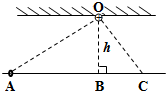 如图所示,水平放置的光滑绝缘杆上B点的正上方O点固定一个带电量为Q=+6.0×10-8C的点电荷,BO相距h=0.24m,B点左侧的A点处套有一个带电量为q=-5.0×10-9C、质量为m=2.0×10-4kg带电小圆环,已知∠OAB=37°.C为杆上B点右侧的另一点,∠OCB=53°.已知由点电荷+Q产生的电场中,距离该点电荷为r处的电势为φ=k$\frac{Q}{r}$,其中k为静电力恒量,k=9.0×109N×m2/C2.(sin37°=0.6,sin53°=0.8).试问:
如图所示,水平放置的光滑绝缘杆上B点的正上方O点固定一个带电量为Q=+6.0×10-8C的点电荷,BO相距h=0.24m,B点左侧的A点处套有一个带电量为q=-5.0×10-9C、质量为m=2.0×10-4kg带电小圆环,已知∠OAB=37°.C为杆上B点右侧的另一点,∠OCB=53°.已知由点电荷+Q产生的电场中,距离该点电荷为r处的电势为φ=k$\frac{Q}{r}$,其中k为静电力恒量,k=9.0×109N×m2/C2.(sin37°=0.6,sin53°=0.8).试问:(1)点电荷Q在A、C三点产生的电势φA、φC分别多大?
(2)将带电小圆环从A点由静止释放,它到达C点时速度多大?
(3)若将圆环带电量改为q′=+1.0×10-8C,并给其一个指向C点的初速度,则初速度v0至少多大才能使其到达C点?
分析 (1)由数学知识得到A、B、C三点到Q点电荷的距离r,由$φ=k\frac{Q}{r}$求出三点的电势.
(2)带电小圆环从A点到C点的过程中,电场力做功qUAC=q(φA-φC),其他力不做功,根据动能定理求解到达C点时速度.
(3)圆环改为带正电后,沿杆向右运动时先要克服电场力做功到达B点,然后电场力做正功使其到达C点,圆环至少要能到达B点,即到达B点时速度应等于零,根据动能定理研究圆环从A到B的过程,求解初速度.
解答 解:(1)根据题给公式$φ=k\frac{Q}{r}$,有
${φ_A}=k\frac{Q}{{\frac{h}{{sin{{37}°}}}}}=k\frac{{Qsin{{37}°}}}{h}=9.0×{10^9}×\frac{{6.0×{{10}^{-8}}×0.6}}{0.24}V=1350V$
${φ_C}=k\frac{Q}{{\frac{h}{{sin{{53}°}}}}}=k\frac{{Qsin{{53}°}}}{h}=9.0×{10^9}×\frac{{6.0×{{10}^{-8}}×0.8}}{0.24}V=1800V$
(2)设圆环到达C点时速度为vC,根据动能定理,有
$q{U_{AC}}=\frac{1}{2}m{v_C}^2$
即$q({{φ_A}-{φ_C}})=\frac{1}{2}m{v_C}^2$
得${v_C}=\sqrt{\frac{{2q({{φ_A}-{φ_C}})}}{m}}=\sqrt{\frac{{2×({-5.0×{{10}^{-9}}})({1350-1800})}}{{2.0×{{10}^{-4}}}}}m/s=0.15m/s$
(3)圆环改为带正电后,沿杆向右运动时先要克服电场力做功到达B点,然后电场力做正功使其到达C点,所以对圆环初速度v0的要求是至少要能到达B点,即到达B点时速度应等于零.
B点的电势:${φ_B}=k\frac{Q}{h}=9.0×{10^9}×\frac{{6.0×{{10}^{-8}}}}{0.24}V=2250V$
根据动能定理,有$q'{U_{AB}}=0-\frac{1}{2}m{v_0}^2$
即$q'({{φ_B}-{φ_A}})=\frac{1}{2}m{v_0}^2$
${v_B}=\sqrt{\frac{{2q'({{φ_B}-{φ_A}})}}{m}}=\sqrt{\frac{{2×1.0×{{10}^{-8}}×({2250-1350})}}{{2.0×{{10}^{-4}}}}}m/s=0.30m/s$
所以初速度v0至少为0.30m/s才能使其到达C点.
答:(1)点电荷Q在A、B、C三点产生的电势φA、φC分别是1350V和1800V.
(2)将带电小圆环从A点由静止释放,它到达C点时速度是0.15m/s.
(3)若将圆环带电量改为qˊ=+1.0×10-8C,初速度v0至少为0.30m/s才能使其到达C点.
点评 本题是信息题,要抓住题给的公式$φ=k\frac{Q}{r}$求解电势,可确定电势差,求出电场力做功.第3问,要注意分析临界条件.

 P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )| A. | P1的平均密度比P2的大 | B. | P1的“第一宇宙速度”比P2的小 | ||
| C. | s1的向心加速度比s2的大 | D. | s1的公转周期比s2的大 |
 如图所示一劲度系数为K的轻质弹簧,上端固定,下端连着一质量为m的物块A,A放在托盘B上,初始时全部静止,弹簧处于自然长度,现设法控制B的运动,使A匀加速下降,用x表示弹簧伸长量,用a表示A的加速度,则在能保持A匀加速下降的整个过程中(始终在弹簧弹性限度内),重力加速度为g,下列说法正确的有( )
如图所示一劲度系数为K的轻质弹簧,上端固定,下端连着一质量为m的物块A,A放在托盘B上,初始时全部静止,弹簧处于自然长度,现设法控制B的运动,使A匀加速下降,用x表示弹簧伸长量,用a表示A的加速度,则在能保持A匀加速下降的整个过程中(始终在弹簧弹性限度内),重力加速度为g,下列说法正确的有( )| A. | B对A的作用力随弹簧伸长量x线性递增 | |
| B. | 若a=$\frac{g}{4}$,则弹簧最大形变量为$\frac{3mg}{4k}$ | |
| C. | B对A的最大作用力为m(g+a) | |
| D. | 物块A的重力势能减少了$\frac{{m}^{2}{g}^{2}}{k}$(g-a) |
| A. | 光电效应实验中,只要入射光足够强,就能产生光电流 | |
| B. | 卢瑟福的α粒子散射实验结果表明电子是原子的组成部分,原子不可再分的观念被打破 | |
| C. | 天然放射现象中的γ射线是原子核受激发产生的 | |
| D. | 放射性元素的半衰期由其原子核内部结构 决定,与外界因素无关 | |
| E. | 氢原子从高能级向低能级跃迁时,放出光子,电势能减少 |
 加利福尼亚大学研制出纳米机器人,研究人员让外层覆盖锌的机器人携带药物进入老鼠体内,机器人到达老鼠的胃部之后,外层的锌与消化液中的盐酸反应,产生氢气气泡作为推进动力,速度可达60μm/s,若机器人所受重力和浮力忽略不计,则下列对机器人在胃液中的运动判断正确的是( )
加利福尼亚大学研制出纳米机器人,研究人员让外层覆盖锌的机器人携带药物进入老鼠体内,机器人到达老鼠的胃部之后,外层的锌与消化液中的盐酸反应,产生氢气气泡作为推进动力,速度可达60μm/s,若机器人所受重力和浮力忽略不计,则下列对机器人在胃液中的运动判断正确的是( )| A. | 纳米机器人由原电池提供的电能直接驱动 | |
| B. | 机器人在胃液中匀速前进时,氢气气泡对机器人做的功与胃液对机器人做的功之和为零 | |
| C. | 机器人前进中对胃液的作用力比胃液对机器人的阻力大 | |
| D. | 机器人在胃液中加速前进的过程中,氢气气泡对机器人做的功等于机器人动能的变化 |
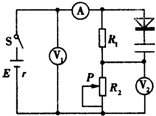 在如图所示的电路中,电源电动势为E,内阻为r,电流表A、二极管和电压表V1、V2均为理想元件,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P向下滑动的过程中( )
在如图所示的电路中,电源电动势为E,内阻为r,电流表A、二极管和电压表V1、V2均为理想元件,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P向下滑动的过程中( )| A. | 电压表V1的示数增大,电压表V2的示数减小 | |
| B. | 电压表V1示数变化量的绝对值与电压表V2示数变化量的绝对值相等 | |
| C. | 电容器上的电压与电流表A示数的比值不变 | |
| D. | 电压表V1示数的变化量与电流表A示数的变化量的比值保持不变 |
| A. | 地震时释放的巨大能量引发海啸,能将震源附近的海水推到几千千米远的地方 | |
| B. | 载人飞船设计时需设法减少发射过程中与航天员身体固有频率相近的超低频振动 | |
| C. | 无线网络信号能绕过障碍物传递到接收终端是利用了干涉原理 | |
| D. | 立体放映机双镜头中的一个镜头发生故障时,观众戴着偏振光眼镜也能体验立体效果 |
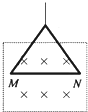
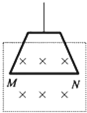
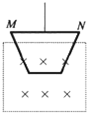
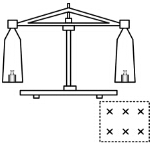 如图所示,用天平测量匀强磁场的磁感应强度,下列各选项所示的载流线圈匝数相同,边长MN相等,将它们分别挂在天平的右臂下方,线圈中通有大小相同的电流,天平处于平衡状态,若磁场发生微小变化,天平最容易失去平衡的是( )
如图所示,用天平测量匀强磁场的磁感应强度,下列各选项所示的载流线圈匝数相同,边长MN相等,将它们分别挂在天平的右臂下方,线圈中通有大小相同的电流,天平处于平衡状态,若磁场发生微小变化,天平最容易失去平衡的是( )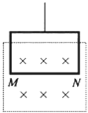
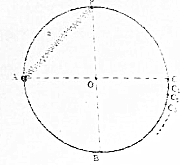 如图所示,一竖直放置的圆环,半径为R,左侧PAB光滑,右侧PCB粗糙,A,C与圆心O等高,轻弹簧a一端固定于最高点O,另一端系一个有孔,质量为m的小球,小球套于圆环上,现将小球置于A点由静止释放,小球第1次经过最低点B时速度为$\sqrt{gR}$,切与圆环刚好无作用力,之后因有摩擦(动摩擦因数较小,但不能忽略)小球能运动到右侧的最高点C1,C2,C3…的高度逐渐降低,重力加速度为g.
如图所示,一竖直放置的圆环,半径为R,左侧PAB光滑,右侧PCB粗糙,A,C与圆心O等高,轻弹簧a一端固定于最高点O,另一端系一个有孔,质量为m的小球,小球套于圆环上,现将小球置于A点由静止释放,小球第1次经过最低点B时速度为$\sqrt{gR}$,切与圆环刚好无作用力,之后因有摩擦(动摩擦因数较小,但不能忽略)小球能运动到右侧的最高点C1,C2,C3…的高度逐渐降低,重力加速度为g.