题目内容
某物体从地面斜向抛出,采用国际单位制时,其位置与时间的函数关系如下:水平方向X=40t;竖直方向Y=-5t2+30t,则以下叙述中正确的量是( )
分析:由小球高度h与运动时间t的关系式h=30t-5t2,令h=0,解得的两值之差便是所要求得的飞行时间的结果;
水平方向的位移x=40t计算;
抛射时的速度为水平分速度与竖直分速度的矢量合.
水平方向的位移x=40t计算;
抛射时的速度为水平分速度与竖直分速度的矢量合.
解答:解:A、由小球高度h与运动时间t的关系式h=30t-5t2,令h=0,解得t=0或者t=6s
两值之差便是所要求得的飞行时间:△t=6-0=6s,故A正确;
B、结合数学知识抛物线解析式当t=-
=3时竖直方向上位移最大,值为:-5×32+30×3=45m,故B错误;
C、水平最大位移:x=40×6=240m,故C错误;
D、抛射时的初速度为40m/s与竖直方向初速度30m/s的矢量合为50m/s,故D错误.
故选:A.
两值之差便是所要求得的飞行时间:△t=6-0=6s,故A正确;
B、结合数学知识抛物线解析式当t=-
| b |
| 2a |
C、水平最大位移:x=40×6=240m,故C错误;
D、抛射时的初速度为40m/s与竖直方向初速度30m/s的矢量合为50m/s,故D错误.
故选:A.
点评:此题考查了二次函数的应用,另外要求我们熟练待定系数法求二次函数解析式的知识,难度一般.

练习册系列答案
相关题目
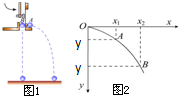 (1)研究平抛运动,下面哪些做法可以减小实验误差
(1)研究平抛运动,下面哪些做法可以减小实验误差

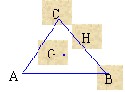
 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上

