题目内容
6.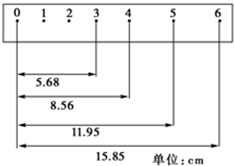 某同学在利用打点计时器研究“匀变速直线运动”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个计数点,每两个相邻的计数点之间还有四个点没标出,其部分相邻点间的距离如图所示,则打下点4时小车的瞬时速度为0.314m/s,小车的加速度为0.510m/s2.(要求计算结果保留三位有效数字)
某同学在利用打点计时器研究“匀变速直线运动”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个计数点,每两个相邻的计数点之间还有四个点没标出,其部分相邻点间的距离如图所示,则打下点4时小车的瞬时速度为0.314m/s,小车的加速度为0.510m/s2.(要求计算结果保留三位有效数字)
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点4的瞬时速度,根据连续相等时间内的位移之差是一恒量,求出小车的加速度.
解答 解:每两个计数点间有四个点没有画出,故两计数点间的时间间隔为:T=5×0.02=0.1s;
计数点4的瞬时速度为:
${v}_{4}=\frac{{x}_{35}}{2T}=\frac{(11.95-5.68)×1{0}^{-2}}{0.2}$m/s=0.314m/s.
根据△x=aT2,a=$\frac{△x}{{T}^{2}}=\frac{[(15.85-11.95)-(11.95-8.56)]×1{0}^{-2}}{0.01}$=0.510m/s2.
故答案为:0.314m/s,0.510m/s2.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用,注意单位换算和有效数字的保留.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 研究某学生骑车返校的速度时可将其视为质点,而对这位学生骑车姿势进行生理学分析时不可将其视为质点 | |
| B. | 如果物体的形状和大小对所研究的问题属于无关或次要因素时,即可把物体看作质点 | |
| C. | 研究地球上物体的运动时,可以选取地面为参考系;而研究地球公转时可以选取太阳为参考系 | |
| D. | 相对于不同的参考系来描述同一个物体的运动其结果一定不同 |
14.足球以1.2m/s的速度水平飞向墙壁,碰到墙壁经0.1s后以0.8m/s的速度沿同一直线反弹回来,足球在与墙壁碰撞的过程中的平均加速度为( )
| A. | 4m/s2,方向垂直墙壁向里 | B. | 4m/s2,方向垂直墙壁向外 | ||
| C. | 20 m/s2,方向垂直墙壁向里 | D. | 20m/s2,方向垂直墙壁向外 |
1.下列带下划线的物体能看做质点的是( )
| A. | 沿着斜面下滑的木块 | B. | 研究刘翔跨栏中的动作 | ||
| C. | 原子核很小,一定能看成质点 | D. | 研究地球的各区域气候变化 |
11.关于自由落体运动,下面说法中正确的是( )
| A. | “亚里士多德认为物体下落快慢是由它们的重量决定的”此观点是正确的 | |
| B. | 伽利略是利用铜球沿阻力很小的斜面滚下来“冲淡”重力的方法来研究x∝t2的 | |
| C. | 秋天的风吹树叶的下落可看做是自由落体运动 | |
| D. | 自由落体运动中“自由”一词只是说初速度为0 |
16.1831年法拉第发现用一块磁铁穿过一个闭合线路时,线路内就会有电流产生,这个效应叫电磁感应.法拉第电磁感应定律可以这样表述:闭合电路中感应电动势的大小( )
| A. | 跟穿过这一闭合电路的磁通量成正比 | |
| B. | 跟穿过这一闭合电路的磁感应强度成正比 | |
| C. | 跟穿过这一闭合电路的磁通量的变化率成正比 | |
| D. | 跟穿过这一闭合电路的磁通量的变化量成正比 |

 某一做直线运动的物体的图象如图所示,根据图象要求:
某一做直线运动的物体的图象如图所示,根据图象要求: 如图,虚线AB右侧是磁感应强度为B1的匀强磁场,左侧是磁感应强度为B2的匀强磁场.已知$\frac{{B}_{1}}{{B}_{2}}$=2.磁场的方向垂直于图中的直面并指向纸面内,现有一带正电的粒子自图中O处以初速度v0开始向右运动.求从开始时刻到第10次通过AB线向右运动的时间内,该粒子在AB方向的平均速度.
如图,虚线AB右侧是磁感应强度为B1的匀强磁场,左侧是磁感应强度为B2的匀强磁场.已知$\frac{{B}_{1}}{{B}_{2}}$=2.磁场的方向垂直于图中的直面并指向纸面内,现有一带正电的粒子自图中O处以初速度v0开始向右运动.求从开始时刻到第10次通过AB线向右运动的时间内,该粒子在AB方向的平均速度.