题目内容
如图所示，一根金属棒MN，质量m=1.0 kg，内阻r=0.50 Ω，水平放置在两根竖直的光滑平行金属导轨上，并始终与导轨保持良好接触。导轨间距为L=0.50 m，导轨下端接一阻值R=2.0 Ω的电阻，导轨电阻不计。在空间内有垂直于导轨平面的磁场，磁感应强度大小只随竖直方向y变化，变化规律B=2.5y。质量M=4.0 kg的物体静止在倾角θ=30°的光滑斜面上，并通过轻质光滑定滑轮和绝缘细绳与金属棒相连接。当金属棒沿y轴方向由静止开始从y=0位置向上运动到h=4.0 m处时，加速度恰好为0。不计空气阻力，斜面和磁场区足够大，g=10 m/s2，求：
（1）金属棒上升到h=4.0 m处时的速度；
（2）金属棒上升h=4.0 m的过程中，电阻R上产生的热量；
（3）金属棒上升h=4.0 m的过程中，通过金属棒横截面的电量。
（1）金属棒上升到h=4.0 m处时的速度；
（2）金属棒上升h=4.0 m的过程中，电阻R上产生的热量；
（3）金属棒上升h=4.0 m的过程中，通过金属棒横截面的电量。
解：（1）当金属棒上升到4m处时
对M有：F=Mgsin30°
对m有：F=mg+F安
F安= BIL，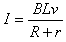
得F安=
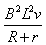
B=2.5y
由以上各式可得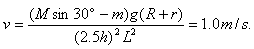
（2）由能量守恒可得：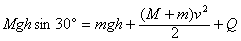
（Q为心路产生的总热量）
得Q=37.5 J
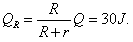
（2）由于
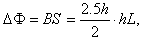得：q=4.0 C
对M有：F=Mgsin30°
对m有：F=mg+F安
F安= BIL，
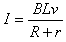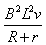
得F安=B=2.5y
由以上各式可得
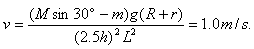
（2）由能量守恒可得：
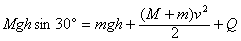（Q为心路产生的总热量）得Q=37.5 J
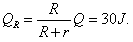
（2）由于
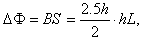得：q=4.0 C 
练习册系列答案
相关题目
如图所示，一根金属棒MN，两端用细软导线连接后悬挂于固定的金属棒PQ上的a、b两点，该导体框处于一足够大的匀强磁场内，该磁场的方向垂直纸面向里．当该磁场强度逐渐增大时，以下判断正确的
如图所示，一根金属棒MN，两端用细软导线连接后水平悬挂于天花板上的a、b两点，棒中通有方向从M流向N的电流．为了增大悬线的弹力，可以在金属棒的中部加一匀强磁场，关于该磁场的方向，以下措施可行的是（ ）
如图所示，一根金属棒MN，两端用细软导线连后悬挂于a、b两点，棒中通有方向从M流向N的电流．为了减小悬线的弹力，可以在金属棒的中部加一匀强磁场，关于该磁场的方向，以下判断正确的是（ ）
