题目内容
如图1所示，一对平行光滑轨道放置在水平面上，两轨道间距l=0.20m，电阻R=1Ω，有一质量为m=1kg的金属棒MN平放在轨道上，与两轨道垂直，金属棒及轨道的电阻可忽略不计，整个装置处于垂直轨道平面向下的匀强磁场中，磁感应强度B=5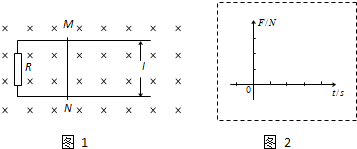
T，现用拉力F平行轨道方向拉金属棒，使棒做初速为零的匀加速直线运动，加速度a=1m/s2，试求：
（1）第2s末安培力FA的大小；
（2）在2虚线方框内画出拉力F随时间t变化的图线（要标出坐标值）；
（3）当拉力F=4N时，电路消耗的电功率；
（4）若拉力F的最大值为5N，流过电阻R的最大电流为多大？
T，现用拉力F平行轨道方向拉金属棒，使棒做初速为零的匀加速直线运动，加速度a=1m/s2，试求：（1）第2s末安培力FA的大小；
（2）在2虚线方框内画出拉力F随时间t变化的图线（要标出坐标值）；
（3）当拉力F=4N时，电路消耗的电功率；
（4）若拉力F的最大值为5N，流过电阻R的最大电流为多大？
分析：（1）求出第二秒末的瞬时感应电动势，由欧姆定律得到感应电流进而得到安培力的大小
（2）求得安培力随时间的变化关系，作出图象
（3）由于棒做初速为零的匀加速直线运动，当拉力F=4N时，可得此时安培力的大小，由安培力表达式可得瞬时电流的大小，从而可得电路消耗的电功率
（4）若拉力F的最大值为5N，则当金属棒做匀速直线运动时，流过电阻R的最大电流为多大，此时外力大小等于安培力大小
（2）求得安培力随时间的变化关系，作出图象
（3）由于棒做初速为零的匀加速直线运动，当拉力F=4N时，可得此时安培力的大小，由安培力表达式可得瞬时电流的大小，从而可得电路消耗的电功率
（4）若拉力F的最大值为5N，则当金属棒做匀速直线运动时，流过电阻R的最大电流为多大，此时外力大小等于安培力大小
解答：
解：（1）棒做初速为零的匀加速直线运动，第2s末的瞬时速度为：
v=at=1×2m/s=2m/s
由安培力公式得：FA=BIl=
=
N=2N
（2）由安培力公式得：FA=BIl=
=
v=v=at=t，故图象为：
（3）棒做初速为零的匀加速直线运动，当拉力F=4N时，可得此时安培力的大小为：F′A=F-ma=4-1×1N=3N
由安培力表达式可得瞬时电流的大小：I′=
=
A=3A
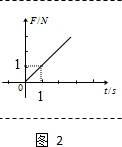电路消耗的电功率：P=I′2R=32×1W=9W
（4）当金属棒做匀速直线运动时，流过电阻R的最大电流为多大，此时外力大小等于安培力大小，故由：
F″A=F=BI″l=5N
解得：I″=5A
答：（1）第2s末安培力FA的大小为2N
（2）在2虚线方框内画出拉力F随时间t变化的图线为：
（3）当拉力F=4N时，电路消耗的电功率为9W
（4）若拉力F的最大值为5N，流过电阻R的最大电流为5N
解：（1）棒做初速为零的匀加速直线运动，第2s末的瞬时速度为：v=at=1×2m/s=2m/s
由安培力公式得：FA=BIl=
| B2l2v |
| R |
| 52×0.22×2 |
| 1 |
（2）由安培力公式得：FA=BIl=
| B2l2v |
| R |
| 52×0.22 |
| 1 |
（3）棒做初速为零的匀加速直线运动，当拉力F=4N时，可得此时安培力的大小为：F′A=F-ma=4-1×1N=3N
由安培力表达式可得瞬时电流的大小：I′=
| F′A |
| Bl |
| 3 |
| 5×0.2 |
电路消耗的电功率：P=I′2R=32×1W=9W（4）当金属棒做匀速直线运动时，流过电阻R的最大电流为多大，此时外力大小等于安培力大小，故由：
F″A=F=BI″l=5N
解得：I″=5A
答：（1）第2s末安培力FA的大小为2N
（2）在2虚线方框内画出拉力F随时间t变化的图线为：
（3）当拉力F=4N时，电路消耗的电功率为9W
（4）若拉力F的最大值为5N，流过电阻R的最大电流为5N
点评：注意安培力公式的导出公式：FA=BIl=
；对金属棒搞好受力分析，应用牛顿第二定律和欧姆定律列方程，这是一个基本的力电综合题，难度适中
| B2l2v |
| R |
练习册系列答案
相关题目
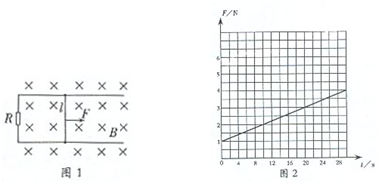
如图1所示，一对平行光滑轨道放置在水平面上，两轨道间距L=0.20m，电阻R=1.0Ω；有一导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻皆可忽略不计，整个装置处于磁感强度B=0.50T的匀强磁场中，磁场方向垂直轨道面向下．现用一拉力F沿轨道方向拉杆，使之做匀加速直线运动，加速度a=2m/s2．设导轨无限长，测得10s末拉力F=3.2N．求：
=0.20m，电阻R=1.0Ω；有一导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻皆可忽略不计，整个装置处于磁感强度B=0.50T的匀强磁场中，磁场方向垂直轨道面向下。现用一外力F沿轨道方向拉杆，做之做匀加速运动，测得力F与时间t的关系如图2所示。求杆的质量m和加速度a。 
