题目内容
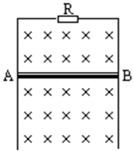 光滑 M 形导轨,竖直放置在垂直于纸面向里的匀强磁场中,已知导轨宽L=0.5m,磁感应强度B=0.2T.有阻值为0.5W的导体棒AB紧挨导轨,沿着导轨由静止开始下落,如图所示,设串联在导轨中的电阻R阻值为2Ω,其他部分的电阻及接触电阻均不计.问:
光滑 M 形导轨,竖直放置在垂直于纸面向里的匀强磁场中,已知导轨宽L=0.5m,磁感应强度B=0.2T.有阻值为0.5W的导体棒AB紧挨导轨,沿着导轨由静止开始下落,如图所示,设串联在导轨中的电阻R阻值为2Ω,其他部分的电阻及接触电阻均不计.问:(1)导体棒AB在下落过程中,产生的感应电流的方向和AB棒受到的磁场力的方向.
(2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各是多少?
分析:(1)根据右手定则判断感应电流的方向,由左手定则判断AB所受的磁场力方向.
(2)根据切割产生的感应电动势公式E=BLv求解感应电动势,由欧姆定律求解感应电流的大小.
(2)根据切割产生的感应电动势公式E=BLv求解感应电动势,由欧姆定律求解感应电流的大小.
解答:解:(1)AB向下切割磁感线,则由右手定则判断可知:AB产生的感应电流方向是A→B,由左手定则判断得知,AB所受的磁场力方向竖直向上.
(2)当导体棒AB的速度为v=5m/s(设并未达到最大速度)时,其感应电动势:?=BLv=0.2×0.5×5=0.5 V
感应电流为:I=
=
(A)=0.2(A)
答:(1)导体棒AB在下落过程中,产生的感应电流的方向是A→B,AB所受的磁场力方向竖直向上..
(2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各0.5V和0.2A.
(2)当导体棒AB的速度为v=5m/s(设并未达到最大速度)时,其感应电动势:?=BLv=0.2×0.5×5=0.5 V
感应电流为:I=
| ε |
| R+r |
| 0.5 |
| 2.5 |
答:(1)导体棒AB在下落过程中,产生的感应电流的方向是A→B,AB所受的磁场力方向竖直向上..
(2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各0.5V和0.2A.
点评:电磁感应中右手定则和左手定则运用时,要注意适用的条件,不能搞乱.

练习册系列答案
相关题目

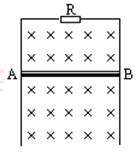
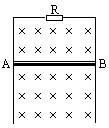 (2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各是多少?
(2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各是多少?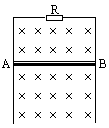 (2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各是多少?
(2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各是多少?