题目内容
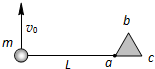（2012?虹口区二模）在光滑水平桌面中央固定一边长为0.3m的小正三棱柱abc，俯视如图．长度为L=1m的细线，一端固定在a点，另一端拴住一个质量为m=0.5kg、不计大小的小球．初始时刻，把细线拉直在ca的延长线上，并给小球以v0=2m/s且垂直于细线方向的水平速度，由于光滑棱柱的存在，细线逐渐缠绕在棱柱上（不计细线与三棱柱碰撞过程中的能量损失）．已知细线所能承受的最大张力为7N，则下列说法中正确的是（ ）分析：细线断裂之前，绳子拉力与速度垂直，小球的速度大小不变．绳子刚断裂时，拉力大小为7N，由F=m
求出此时的半径．小球每转120°半径减小0.3m，确定出小球转动的圈数，求出时间．根据初位置、末位置的直线距离求解位移大小．
| v2 |
| r |
解答：解：A、B细线断裂之前，绳子拉力与速度垂直，不做功，不改变小球的速度大小，故小球的速度大小保持不变．故A正确，B错误．
C、绳子刚断裂时，拉力大小为7N，由F=m
得，此时的半径为r=
m，由于小球每转120°半径减小0.3m，则知小球刚好转过一周，细线断裂，则小球运动的总时间为
t=
?
+
?
+
?
而r1=1m，r2=0.7m，r3=0.4m，v0=2m/s，解得，t=0.7π s．故C正确．
D、小球每转120°半径减小0.3m，细线断裂之前，小球运动的位移大小为1m-0.1m=0.9m．故D正确．
故选ACD
C、绳子刚断裂时，拉力大小为7N，由F=m
| ||
| r |
| 2 |
| 7 |
t=
| 1 |
| 3 |
| 2πr1 |
| v0 |
| 1 |
| 3 |
| 2πr2 |
| v0 |
| 1 |
| 3 |
| 2πr3 |
| v0 |
而r1=1m，r2=0.7m，r3=0.4m，v0=2m/s，解得，t=0.7π s．故C正确．
D、小球每转120°半径减小0.3m，细线断裂之前，小球运动的位移大小为1m-0.1m=0.9m．故D正确．
故选ACD
点评：本题是物理数列类型，通过分析，抓住小球每转120°半径减小0.3m，确定出小球转动的圈数是关键．
练习册系列答案
相关题目
（2012?虹口区二模）如图所示，在柱形容器中装有部分水，容器上方有一可自由移动的活塞．容器水面浮有一个木块和一个一端封闭、开口向下的玻璃管，玻璃管中有部分空气，系统稳定时，玻璃管内空气柱在管外水面上方的长度为a，空气柱在管外水面下方的长度为b，水面上方木块的高度为c，水面下方木块的高度为d．现在活塞上方施加竖直向下、且缓缓增大的力F，使活塞下降一小段距离（未碰及玻璃管和木块），下列说法中正确的是（ ）
（2012?虹口区二模）在水平放置的光滑绝缘杆ab上，挂有两个金属环M和N，两环套在一个通电密绕长螺线管的中部，螺线管中部区域的管外磁场可以忽略．当变阻器的滑动头向左移动时，两环的运动情况是（ ）