题目内容
如右图所示为某同学设计的节能运输系统.斜面轨道的倾角为37°,木箱与轨道之间的动摩擦因数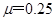 .设计要求:木箱在轨道顶端时,自动装货装置将质量
.设计要求:木箱在轨道顶端时,自动装货装置将质量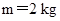 的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取
的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取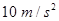 ,sin 37°=0.6 ,cos 37°=0.8.求:
,sin 37°=0.6 ,cos 37°=0.8.求:
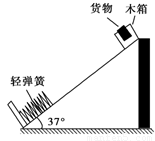
(1)离开弹簧后,木箱沿轨道上滑的过程中的加速度大小;
(2)满足设计要求的木箱质量.
(1) 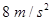 (2)2 kg
(2)2 kg
【解析】
试题分析:(1)设木箱质量为m′,对木箱的上滑过程,由牛顿第二定律有:
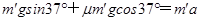 ,代入数据解得:a=
,代入数据解得:a=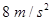 .
.
(2)设木箱沿轨道下滑的最大距离为L,弹簧被压缩至最短时的弹性势能为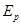 ,根据能量守恒定律:货物和木箱下滑过程中有:
,根据能量守恒定律:货物和木箱下滑过程中有: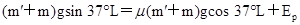
木箱上滑过程中有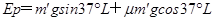
联立代入数据解得: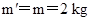 .
.
考点:考查了牛顿第二定律,能量守恒定律的应用
点评:解决本题的关键掌握牛顿第二定律,会用牛顿第二定律求加速度.以及选择合适的研究过程,运用能量守恒.

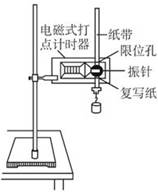
在验证机械能守恒定律的实验中,已知电磁打点计时器工作周期T=0.02s,自由下落的重锤质量m=2kg,如图所示为某同学实验后选出的一条理想的纸带,O点是自由落体的第一个点,A、B、C是在纸带上取出的三个计数点,AB、BC间各有一个点未画出。经测得A、B、C三点到O点的距离分别为:S1=12.90cm,S2=20.60cm,S3=28.90cm,g=10m/s2,完成以下问题:(本题中的数值计算,结果均保留两位有效数字)
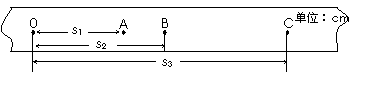 |
①纸带的______端与重锤连接(填左或右)。
②打点计时器打下计数点B时,物体的速度vB=_________m/s。
③从起点O到打下计数点B的过程中,重力势能的减少量△EP=________J,此过程中物体动能的增量△EK=__________J。
④在此实验中发现,重锤重力势能的减少量总是大于动能的增加量,其主要原因是因为在重锤下落过程存在阻力作用,可以通过该装置测定该阻力的大小。设重锤所受阻力大小F恒定,试用题目中所给物理量的符号表示出重锤所受阻力大小F=____________。(用m、T、g、S1、S2、S3表示)

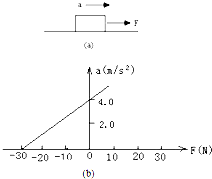 如图所示,某同学做了如下的力学实验,一个质量为m的物体A在水平面上运动,A受到向右的拉力F作用.设水平向右为加速度a的正方向,如图(a)所示,测得A 的加速度a与拉力F之间的关系如图(b )所示.由图象可知,A 的质量m=
如图所示,某同学做了如下的力学实验,一个质量为m的物体A在水平面上运动,A受到向右的拉力F作用.设水平向右为加速度a的正方向,如图(a)所示,测得A 的加速度a与拉力F之间的关系如图(b )所示.由图象可知,A 的质量m=