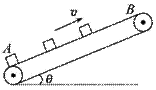题目内容
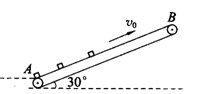
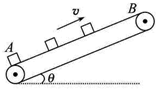 传送带用于传送工件可以提高工作效率.如图所示,传送带长度是l,以恒定的速度v运送质量为m的工件,工件从最低点A无初速度地放到传送带上,到达最高点B前有一段匀速的过程.工件与传送带之间的动摩擦因数为μ,传送带与水平方向夹角为θ,每当前一个工件在传送带上停止相对滑动时,后一个工件立即放到传送带上,整条传送带满载时恰好能传送n个工件.重力加速度为g,则下列说法正确的是( )
传送带用于传送工件可以提高工作效率.如图所示,传送带长度是l,以恒定的速度v运送质量为m的工件,工件从最低点A无初速度地放到传送带上,到达最高点B前有一段匀速的过程.工件与传送带之间的动摩擦因数为μ,传送带与水平方向夹角为θ,每当前一个工件在传送带上停止相对滑动时,后一个工件立即放到传送带上,整条传送带满载时恰好能传送n个工件.重力加速度为g,则下列说法正确的是( )A、在传送带上摩擦力对每个工件做的功为Wf=
| ||
B、在传送带上摩擦力对每个工件做的功为Wf=
| ||
C、每个工件与传送带之间由摩擦产生的热量为Q=
| ||
| D、传送带满载工件比空载时增加的功率为P=mgv(μcosθ+nsinθ-sinθ) |
分析:工件先受到滑动摩擦力,大小为μmgcosθ,后速度与传送带相同后,受到静摩擦力,大小为mgsinθ,根据功的公式求解摩擦力对每个工件做的功.摩擦生热Q=fs相,s相是工件与传送带的相对位移.电动机多消耗的电能转化为工件的机械能与克服摩擦力做功转化成的内能,根据能量守恒求解.
解答:解:对物体,由牛顿第二定律得:
F2-mgsinθ=ma ①
F1-mgcosθ=0 ②
又摩擦力 F2=μF1
得:a=g(μcosθ-sinθ)
工件在传送带上停止相对滑动时有:
v=at
得:t=
位移S=
at2=
皮带位移S1=vt=
工件相对于皮带的位移S2=S1-S=
摩擦力对每个工件做的功W=μmgS2cosθ+mgsinθ(l-S)=mg(μcosθ-sinθ)S+mglsinθ=
mv2+mglsinθ;故B正确;A错误;
C、摩擦产生的内能Q=μmgcosθ?S2=
cosθ;故C错误;
D、满载时皮带上工件数n个,其中(n-1)个在做匀速直线运动,最下面的一个正在做匀加速运动且加速到最大速度时功率最大,
所以增加的功率P=(n-1)mgvsinθ+F2?v=(n-1)mgvsinθ+(mgsinθ+mgμcosθ-mgsinθ)v=mgv(μcosθ+nsinθ-sinθ),故D正确;
故选:BD.
F2-mgsinθ=ma ①
F1-mgcosθ=0 ②
又摩擦力 F2=μF1
得:a=g(μcosθ-sinθ)
工件在传送带上停止相对滑动时有:
v=at
得:t=
| v |
| a |
位移S=
| 1 |
| 2 |
| v2 |
| 2g(μcosθ-sinθ) |
皮带位移S1=vt=
| v2 |
| a |
工件相对于皮带的位移S2=S1-S=
| v2 |
| 2g(μcosθ-sinθ) |
摩擦力对每个工件做的功W=μmgS2cosθ+mgsinθ(l-S)=mg(μcosθ-sinθ)S+mglsinθ=
| 1 |
| 2 |
C、摩擦产生的内能Q=μmgcosθ?S2=
| μmgv2 |
| 2g(μcosθ-sinθ) |
D、满载时皮带上工件数n个,其中(n-1)个在做匀速直线运动,最下面的一个正在做匀加速运动且加速到最大速度时功率最大,
所以增加的功率P=(n-1)mgvsinθ+F2?v=(n-1)mgvsinθ+(mgsinθ+mgμcosθ-mgsinθ)v=mgv(μcosθ+nsinθ-sinθ),故D正确;
故选:BD.
点评:本题一方面要分析工件的运动情况,由牛顿第二定律和运动学公式结合求解相对位移,即可求出摩擦产生的热量,另一方面要分析能量如何转化,由能量守恒定律求解电动机消耗的电能.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
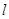 ,以恒定的速度v运送质量为m的工件,工件从最低点A无初速度地放到传送带上,到达最高点B前有一段匀速的过程.工件与传送带之间的动摩擦因数为μ,传送带与水平方向夹角为θ,每当前一个工件在传送带上停止相对滑动时,后一个工件立即放到传送带上,整条传送带满载时恰好能传送n个工件.重力加速度为g,则下列说法正确的是( )
,以恒定的速度v运送质量为m的工件,工件从最低点A无初速度地放到传送带上,到达最高点B前有一段匀速的过程.工件与传送带之间的动摩擦因数为μ,传送带与水平方向夹角为θ,每当前一个工件在传送带上停止相对滑动时,后一个工件立即放到传送带上,整条传送带满载时恰好能传送n个工件.重力加速度为g,则下列说法正确的是( )
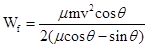
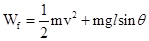
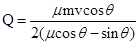
 =
=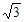 /2,传送带与水平方向夹角是θ= 30o,传送带A、B间长度是l = 16m;每当前一个工件在传送带上停止相对滑动时,后一个工件立即放到传送带上,取g = 10m/s2,求:
/2,传送带与水平方向夹角是θ= 30o,传送带A、B间长度是l = 16m;每当前一个工件在传送带上停止相对滑动时,后一个工件立即放到传送带上,取g = 10m/s2,求: