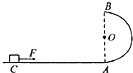题目内容
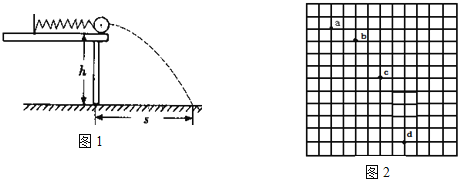
【题目】在“探究弹性势能表达式”时,一位同学设计了如图1所示装置,以研究轻质弹簧的弹性势能与弹簧长度改变量的关系.实验过程如下:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘.让小钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,并落到水平地面上,钢球水平位移记为s.
(1)依据能的转化与守恒思想,小球平抛时具有的初动能______ (选填“大于”、“小于”或“等于”)小球释放前弹簧储存的弹性势能
(2)若增大弹簧的压缩量,小球飞行的水平距离将变大,请你推导出弹簧弹性势能Ep与小钢球质量m、桌面离地高度h、水平距离s、重力加速度g的关系式:______ .
(3)图2为一张印有小方格的纸,记录着实验中钢球的某次运动轨迹,图中a、b、c、d四点为小球平抛时经过的四个位置.小方格的边长L=1.25cm.则小球平抛初速度的计算式为v0= ______ (用L、g表示).
【答案】 等于 ![]()
![]()
【解析】
(1)根据机械能守恒定律可明确动能和弹性势能的关系;
(2)根据高度求出平抛运动的时间,结合水平位移和时间求出小钢球飞出桌面的速度.
根据能量守恒求出弹簧弹性势能与小钢球质量m、桌面离地高度h、水平距离s、重力加速度g的关系式;
(3)根据竖直方向的位移,结合y=gT2求解时间T,然后根据水平位移求解水平速度.
(1)由机械能守恒定律可知,小球飞出时的动能由弹簧的弹性势能转化而来,二者应相等;
(2) 根据平抛运动可知![]()
根据能量守恒得,![]() .
.
(3)设相邻两点间的时间间隔为T,
竖直方向:3L-L=gT2,得到![]()
水平方向: ![]()

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目