题目内容
 如图所示,设质量为m的物体在空中做斜抛运动,在高度为h1的Q处运动速度为v1,在高度为h2的R处运动速度为v2,试由动能定理推导出物体在Q处的机械能等于物体在R处的机械能.(取水平面ab为重力势能的参考平面)
如图所示,设质量为m的物体在空中做斜抛运动,在高度为h1的Q处运动速度为v1,在高度为h2的R处运动速度为v2,试由动能定理推导出物体在Q处的机械能等于物体在R处的机械能.(取水平面ab为重力势能的参考平面)分析:根据动能定理和重力做功与重力势能的变化关系公式列式后联立分析即可.
解答:解:研究质量为m的物体,分析物体受力:物体在运动中只受重力作用.
根据动能定理W=△Ek,且重力做功与路径无关.
有:mg(h1-h2)=
m
-
m
整理,有:mgh1+
m
=mgh2+
mv
由上式可知:物体在Q处的动能与势能之和等于物体在R处的动能与势能之和,
即:物体在Q处的机械能等于物体在R处的机械能;
答:证明如上.
根据动能定理W=△Ek,且重力做功与路径无关.
有:mg(h1-h2)=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
整理,有:mgh1+
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
2 2 |
由上式可知:物体在Q处的动能与势能之和等于物体在R处的动能与势能之和,
即:物体在Q处的机械能等于物体在R处的机械能;
答:证明如上.
点评:本题是通过斜抛运动证明机械能守恒定律的问题,关键明确动能定理和重力做功与重力势能关系,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
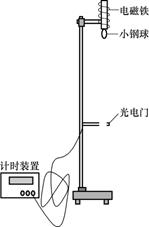
 物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如下图的实验装置.
物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如下图的实验装置. (Ⅰ)物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如图的实验装置.
(Ⅰ)物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如图的实验装置.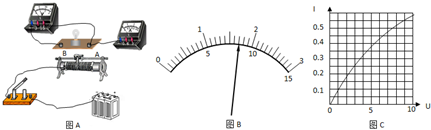
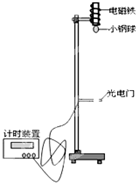 物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如下图的实验装置.
物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如下图的实验装置.